Проверка на зацикленность

Рассмотрим теперь алгоритм, проверяющий, является ли корректной система семантических правил, определeнная в предыдущем разделе. Другими словами, мы хотим знать, когда семантические правила позволяют вычислить значение любого атрибута любого узла произвольного дерева вывода. Можно считать, что грамматика не содержит "бесполезных" правил вывода, то есть что каждое правило из P участвует в выводе хотя бы одной терминальной цепочки.

Пусть T - произвольное дерево вывода, соответствующее данной грамматике; метками концевых узлов могут быть только терминальные символы, корню же разрешим иметь меткой не только аксиому, но и любой символ из V . Тогда можно определить ориентированный граф D(T), соответствующий T, взяв в качестве его узлов упорядоченные пары (X,

), где X - узел дерева T, а - атрибут символа, служащего меткой узла X. Дуга из (X1; 1) в (X2, 2) проводится в том и только в том случае, когда семантическое правило, вычисляющее атрибут 2, непосредственно использует значение атрибута 1. Например, если T - дерево (рис. 1.2), а в качестве семантических правил взяты правила (таблица 1.1), то орграф D(T) будет иметь такой вид:

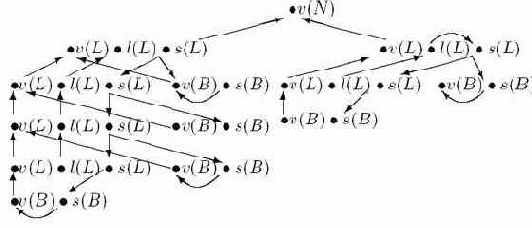
Рис. 3.1. 

Другими словами, узлами графа D(T) служат атрибуты, значения которых нужно вычислить, а дуги определяют зависимости, подразумевающие, какие атрибуты вычисляются раньше, а какие позже (рис. 1.6).

Ясно, что семантические правила являются корректными тогда и только тогда, когда ни один из орграфов D(T) не содержит ориентированного цикла. Дело в том, что если в графе нет ориентированных циклов, то можно применить хорошо известную процедуру, позволяющую присвоить значения всем атрибутам. Если же в некотором графе D(T) есть ориентированный цикл, то ввиду того что грамматика не содержит бесполезных правил, можно утверждать, что существует ориентированный цикл в некотором графе D(T), у которого меткой корня дерева T служит S. Для такого дерева T все атрибуты вычислить не уда_тся. Таким образом, задача "Являются ли семантические правила корректным?" сводится к задаче "Содержат ли орграфы D(T) ориентированные циклы?"

Каждый орграф D(T) можно рассматривать как суперпозицию меньших орграфов Dp, соответствующих правилам Xp0 Xp1 ... Xpn грамматики, 1 p m. В обозначениях разд. 2 орграф Dp имеет узлы (Xpj, ) для 0 j np, A(Xpj) и дуги из (Xpki , ) в (Xpj , ) для 0 j np, A0(Xpj), если j = 0, A1(Xpj ), если j > 0, ki = ki(p, j, ), i = i(p, j, ), 1 i t(p, j, ). Другими словами, Dp отражает связи, которые порождают все семантические правила, соответствующие p-му синтаксическому правилу. Например, шести правилам грамматики (таблица 1.1) соответствуют шесть следующих орграфов:


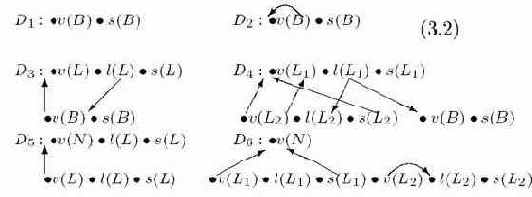
Рис. 3.2. 

Орграф (рис. 3.1) получается в результате "объединения" таких подграфов. Вообще, если T имеет в качестве метки корня терминал, D(T) не содержит дуг. Если корень дерева T помечен нетерминальным символом, T имеет вид


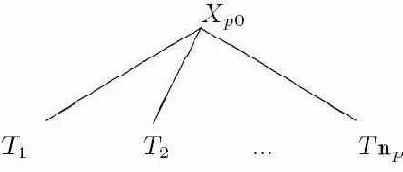
Рис. 3.3. 

для некоторого p, где Tj - дерево вывода, у которого корень помечен символом Xpj, где 1 j np. В первом случае говорят, что T - дерево вывода типа 0, во втором случае T называется деревом вывода типа р. В соответствии с этим определением для того, чтобы по Dp, D(T1), ... , D(Tnp ) построить D(T), нужно для всех j, 1 j np совместить узлы, соответствующие атрибутам символа Xpj графа Dp с соответствующими узлами (отвечающими тем же атрибутам корня дерева Tj) в графе D(Tj ).

Для проверки того, содержит ли граф D(T) ориентированный цикл, нам понадобится ещe одно понятие. Пусть p - номер правила вывода. Обозначим через Gj

произвольный орграф (1 j np), множество узлов которого является подмножеством множества A(Xpj) атрибутов символа Xpj. Пусть

Dp[G1,..., Gnp ]

Пример 3.4.

(html, txt)

орграф, полученный из Dp добавлением дуг, идущих из (Xpj, ) в (Xpj, 0), если в графе Gj есть дуга из в 0

Например, если



и если D4 - ориентированный граф из (3.2), то D4(G1, G2) имеет вид


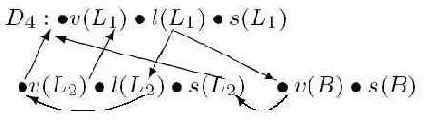
Рис. 3.4. 

Теперь можно воспользоваться следующим алгоритмом. Для любого X V S(X) будет некоторым множеством ориентированных графов с узлами из A(X). Сначала для всех X N S(X) пусто, а для X = N S(X) состоит из единственного графа с множеством узлов A(X) и не содержащего дуг.


Будем добавлять к множествам S(X) новые орграфы при помощи следующей процедуры до тех пор, пока в S(X) не перестанут появляться новые элементы. Выберем целое p; 1 p m и для каждого j, 1 j np, выберем орграф D0j S(Xpj). Затем добавим в S(Xp0) орграф с множеством узлов A(Xpo), обладающий тем свойством, что в нeм дуга от к 0 идeт тогда и только тогда, когда в орграфе

(3.5)

существует ориентированный путь из (Xp0; ) в (Xp0; '): Ясно, что этот процесс рано или поздно закончится и новые орграфы перестанут порождаться, поскольку вообще существует лишь конечное число ориентированных графов. В случае грамматики (таблица 1.1) алгоритм построит следующие множества:



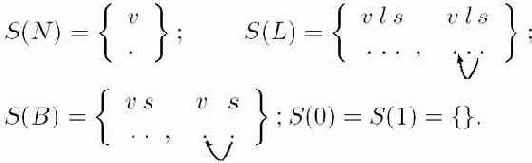
Пусть T - дерево вывода с корнем X, и пусть D'(T) - ориентированный граф с множеством узлов A(X), у которого есть дуга из в ' тогда и только тогда, когда в D(T) существует ориентированный путь из (X, ) в (X, '). Покажем, что после окончания работы описанного выше алгоритма для всех X V S(X) - это множество всех D'(T), где T - дерево вывода с корнем X 1)

. Действительно, построение не добавляет к S(X) новых ориентированных графов, не являющихся D'(T). Алгоритм можно даже легко обобщить так, чтобы для каждого графа из S(X) он печатал на выходе соответствующее дерево вывода T. Обратно, если T - дерево вывода, мы можем показать индукцией по числу узлов дерева T, что D'(T) принадлежит некоторому множеству S(X). В противном случае T должно иметь вид (3.3) и D(T) "составлен" из . По индукции и вследствие того, что при j j' из D(Tj) в D(Tj' ) не проходит дуг вне Dp, дуги в , составляющей рассматриваемый путь графа D(T), можно заменить соответствующими дугами в , где . Поэтому ориентированный граф, включаемый в S(Xp0) на базе , просто совпадает с D'(T).

Вышеприведeнный алгоритм решает задачу, поставленную в этом разделе.

Теорема. Семантические правила, добавленные к грамматике так, как это сделано в разд. 2, являются корректными тогда и только тогда, когда ни один из ориентированных графов (3.5) ни при каком выборе p и не содержит ориентированных циклов.

Доказательство. Если (3.5) содержит ориентированный цикл, то, как было показано выше, некоторый D(T) содержит ориентированный цикл. Наоборот, если T - дерево с наименьшим возможным числом улов, такое, что D(T) содержит ориентированный цикл, то T должно иметь вид (рис. 3.3), а D(T) "составляется" из . Из минимальности T следует, что ориентированный цикл включает по меньшей мере одну дугу графа Dp, и, следовательно, можно, рассуждая, как выше, все дуги, образующие этот цикл и лежащие в одном из графов , заменить дугами графа (3.5).


Содержание раздела

---

---

---

Главная сайта

---