Определение атрибутных грамматик

Атрибутной грамматикой называется четверка AG = (G, AS, AI, R), где

G = (N, T, P, S) - приведенная КС-грамматика;
AS - конечное множество синтезируемых атрибутов;
AI - конечное множество наследуемых атрибутов, AS
AI =
;
R - конечное множество семантических правил.

Атрибутная грамматика AG сопоставляет каждому символу X из N

T множество AS(X) синтезируемых атрибутов и множество AI (X) наследуемых атрибутов. Множество всех синтезируемых атрибутов всех символов из N

T обозначается AS, наследуемых - AI . Атрибуты разных символов являются различными атрибутами. Будем обозначать атрибут a символа X как a(X). Значения атрибутов могут быть произвольных типов, например, представлять собой числа, строки, адреса памяти и т.д.

Пусть правило p из P имеет вид X0

X1X2 ... Xn. Атрибутная грамматика AG сопоставляет каждому правилу p из P конечное множество R(p) семантических правил вида

a(Xi) = f(b(Xj), c(Xk), ... , d(Xm))

где 0

j, k, ... , m

n, причем 1

n, если

(то есть a(Xi) - наследуемый атрибут), и i = 0, если

(то есть a(Xi) - синтезируемый атрибут).

Таким образом, семантическое правило определяет значение атрибута a символа Xi на основе значений атрибутов b, c, . . . , d символов Xj , Xk, . . . , Xm соответственно.

В частном случае длина n правой части правила может быть равна нулю, тогда будем говорить, что атрибут a символа Xi "получает в качестве значения константу".

В дальнейшем будем считать, что атрибутная грамматика не содержит семантических правил для вычисления атрибутов терминальных символов. Предполагается, что атрибуты терминальных символов - либо предопределенные константы, либо доступны как результат работы лексического анализатора.

Пример 5.5. Рассмотрим атрибутную грамматику, позволяющую вычислить значение вещественного числа, представленного в десятичной записи. Здесь N = {Num, Int, Frac}, T = {digit, .}, S = Num, а правила вывода и семантические правила определяются следующим образом (верхние индексы используются для ссылки на разные вхождения одного и того же нетерминала):

Для этой грамматики

Пусть дана атрибутная грамматика AG и цепочка, принадлежащая языку, определяемому соответствующей G = (N, T, P, S). Сопоставим этой цепочке "значение "следующим образом. Построим дерево разбора T этой цепочки в грамматике G. Каждый внутренний узел этого дерева помечается нетерминалом X0, соответствующим применению p-го правила грамматики; таким образом, у этого узла будет n непосредственных потомков (рис. 5.2).

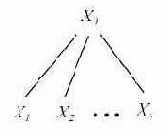
Рис. 5.2.

Пусть теперь X - метка некоторого узла дерева и пусть a - атрибут символа X. Если a - синтезируемый атрибут, то X = X0 для некоторого

; если же a - наследуемый атрибут, то X = Xj для некоторых

и 1

n. В обоих случаях дерево "в районе" этого узла имеет вид, приведенный на рис. 5.2. По определению, атрибут a имеет в этом узле значение v, если в соответствующем семантическом правиле

a(Xi) = f(b(Xj), c(Xk), ... , d(Xm))

все атрибуты b, c, . . . , d уже определены и имеют в узлах с метками Xj , Xk, . . . , Xm значения vj , vk, . . . , vm соответственно, а v = f(v1, v2, ... , vm). Процесс вычисления атрибутов на дереве продолжается до тех пор, пока нельзя будет вычислить больше ни одного атрибута. Вычисленные в результате атрибуты корня дерева представляют собой "значение", соответствующее данному дереву вывода.

Заметим, что значение синтезируемого атрибута символа в узле синтаксического дерева вычисляется по атрибутам символов в потомках этого узла; значение наследуемого атрибута вычисляется по атрибутам "родителя" и "соседей".

Атрибуты, сопоставленные вхождениям символов в дерево разбора, будем называть вхождениями атрибутов в дерево разбора, а дерево с сопоставленными каждой вершине атрибутами - атрибутированным деревом разбора.

Пример 5.6. Атрибутированное дерево для грамматики из предыдущего примера и цепочки w = 12:34 показано на рис. 5.3.

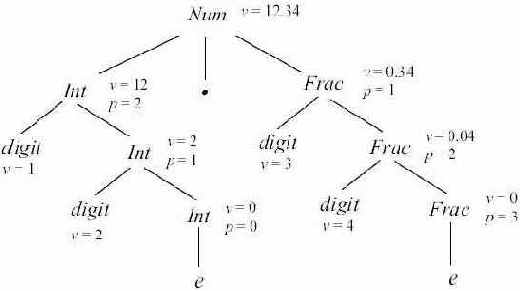
Рис. 5.3.

Будем говорить, что семантические правила заданы корректно, если они позволяют вычислить все атрибуты произвольного узла в любом дереве вывода.

Между вхождениями атрибутов в дерево разбора существуют зависимости, определяемые семантическими правилами, соответствующими примененным синтаксическим правилам. Эти зависимости могут быть представлены в виде ориентированного графа следующим образом.

Пусть T - дерево разбора. Сопоставим этому дереву ориентированный граф D(T), узлами которого являются пары (n; a), где n - узел дерева T, a - атрибут символа, служащего меткой узла n. Граф содержит дугу из (n1, a1) в (n2, a2) тогда и только тогда, когда семантическое правило, вычисляющее атрибут a2, непосредственно использует значение атрибута a1. Таким образом, узлами графа D(T) являются атрибуты, которые нужно вычислить, а дуги определяют зависимости, подразумевающие, какие атрибуты вычисляются раньше, а какие позже.

Пример 5.7. Граф зависимостей атрибутов для дерева разбора из предыдущего примера показан на рис. 5.4.

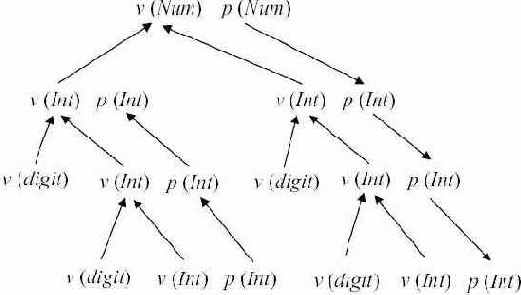
Рис. 5.4.

Можно показать, что семантические правила являются корректными тогда и только тогда, когда для любого дерева вывода T соответствующий граф D(T) не содержит циклов (то есть является ориентированным ациклическим графом).

Содержание раздела