Теория и реализация языков программирования
       

Построение недетерминированного конечного автомата по регулярному выражению


Рассмотрим алгоритм построения по регулярному выражению недетерминированного конечного автомата, допускающего тот же язык.

Алгоритм 3.1. Построение недетерминированного конечного автомата по регулярному выражению.

Вход. Регулярное выражение r в алфавите T.

Выход. НКА M, такой что L(M) = L(r).

Метод. Автомат для выражения строится композицией из автоматов, соответствующих подвыражениям. На каждом шаге построения строящийся автомат имеет в точности одно заключительное состояние, в начальное состояние нет переходов из других состояний и нет переходов из заключительного состояния в другие.

  1. Для выражения e строится автомат


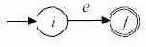
    Рис. 3.5. 

  2. Для выражения
    строится автомат
  3. Пусть M(s) и M(t) - НКА для регулярных выражений s и t соответственно.


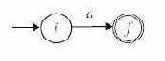
    Рис. 3.6. 

    1. Для выражения s|t автомат M(s|t) строится как показано на рис. 3.7. Здесь i - новое начальное состояние и f - новое заключительное состояние. Заметим, что имеет место переход по e из i в начальные состояния M(s) и M(t) и переход по e из заключительных состояний M(s) и M(t) в f. Начальное и заключительное состояния автоматов M(s) и M(t) не являются таковыми для автомата M(s|t).


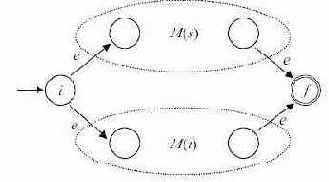
      Рис. 3.7. 

    2. Для выражения st автомат M(st) строится следующим образом:


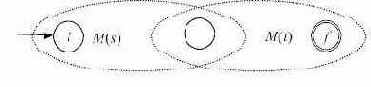
      Рис. 3.8. 

      Начальное состояние автомата M(s) становится начальным для нового автомата, а заключительное состояние M(t) становится заключительным для нового автомата. Начальное состояние M(t) и заключительное состояние M(s) сливаются, то есть все переходы из начального состояния M(t) становятся переходами из заключительного состояния M(s). В новом автомате это объединенное состояние не является ни начальным, ни заключительным.

    3. Для выражения s* автомат M(s*) строится следующим образом:


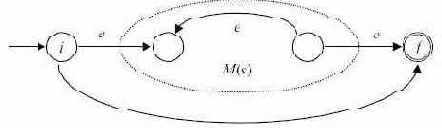
      Рис. 3.9. 

      Здесь i - новое начальное состояние, а f - новое заключительное состояние.



Содержание раздела