Теория и реализация языков программирования
Построение детерминированного конечного автомата по недетерминированному
Рассмотрим алгоритм построения по недетерминированному конечному автомату детерминированного конечного автомата, допускающего тот же язык.
Алгоритм 3.2. Построение детерминированного конечного автомата по недетерминированному.
Вход. НКА M = (Q, T, D, q0, F).
Выход. ДКА

Метод. Каждое состояние результирующего ДКА - это некоторое множество состояний исходного НКА.
В алгоритме будут использоваться следующие функции:




Вначале Q' и D' пусты. Выполнить шаги 1-4:
(1) Определить

(2) Добавить

(3) Выполнить следующую процедуру:

(4) Определить

Пример 3.6. Результат применения алгоритма 3.2 приведен на рис. 3.10.
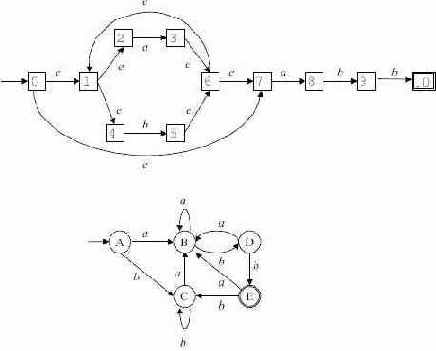
Рис. 3.10.
Приведем теперь алгоритм построения по регулярному выражению детерминированного конечного автомата, допускающего тот же язык [?].
Пусть дано регулярное выражение r в алфавите T. К регулярному выражению r добавим маркер конца: (r)#. Такое регулярное выражение будем называть пополненным. В процессе своей работы алгоритм будет использовать пополненное регулярное выражение.
Алгоритм будет оперировать с синтаксическим деревом для пополненного регулярного выражения (r)# , каждый лист которого помечен символом

Каждому листу дерева (кроме e-листьев) присвоим уникальный номер, называемый позицией, и будем использовать его, с одной стороны, для ссылки на лист в дереве, и, с другой стороны, для ссылки на символ, соответствующий этому листу. Заметим, что если некоторый символ используется в регулярном выражении несколько раз, он имеет несколько позиций.
Обойдем дерево T снизу-вверх слева-направо и вычислим четыре функции: nullable,firstpos, lastpos и followpos. Три первые функции - nullable, firstpos и lastpos - определены на узлах дерева, а followpos - на множестве позиций. Значением всех функций, кроме nullable, является множество позиций. Функция followpos вычисляется через три остальные функции.
Функция firstpos(n) для каждого узла n синтаксического дерева регулярного выражения дает множество позиций, которые соответствуют первым символам в подцепочках, генерируемых подвыражением с вершиной в n. Аналогично, lastpos(n) дает множество позиций, которым соответствуют последние символы в подцепочках, генерируемых подвыражениями с вершиной n. Для узла n, поддеревья которого (то есть деревья, у которых узел n является корнем) могут породить пустое слово, определим nullable(n)=true, а для остальных узлов nullable(n)=false.
Таблица для вычисления функций nullable, firstpos и lastpos приведена на рис. 3.11.
Пример 3.7. На рис. 3.12 приведено cинтаксическое дерево для пополненного регулярного выражения (a|b)*abb# с результатом вычисления функций firstpos и lastpos. Слева от каждого узла расположено значение firstpos, справа от узла - значение lastpos. Заметим, что эти функции могут быть вычислены за один обход дерева.
Если i - позиция, то followpos(i) есть множество позиций j таких, что существует некоторая строка ... cd ..., входящая в язык, описываемый регулярным выражением, такая, что позиция i соответствует этому вхождению c, а позиция j - вхождению d.

Рис. 3.11.

Рис. 3.12.

Рис. 3.13.
Рассмотрим теперь алгоритм построения ДКА с минимальным числом состояний, эквивалентного данному ДКА [?].
Пусть M = (Q, T, D, q0, F) - ДКА. Будем называть M всюду определенным, если D(q, a)




Лемма. Пусть M = (Q, T, D, q0, F) - ДКА, не являющийся всюду определенным. Существует всюду определенный ДКА M', такой что L(M) = L(M').
Доказательство. Рассмотрим автомат

где q'

(1) Для всех




(2) Для всех



(3) Для всех

Легко показать, что автомат M' допускает тот же язык, что и M.
Приведенный ниже алгоритм получает на входе всюду определенный автомат. Если автомат не является всюду определенным, его можно сделать таковым на основании только что приведенной леммы.
Алгоритм 3.4. Построение ДКА с минимальным числом состояний.
Вход. Всюду определенный ДКА M = (Q, T, D, q0, F).
Выход. ДКА

Метод. Выполнить шаги 1-5:
(1) Построить начальное разбиение ? множества состояний из двух групп: заключительные состояния Q и остальные Q - F, то есть ? = {F, Q - F}.
(2) Применить к ? следующую процедуру и получить новое разбиение ?new:
for (каждой группы G в ?){ разбить G на подгруппы так, чтобы состояния s и t из G оказались в одной подгруппе тогда и только тогда, когда для каждого входного символа a состояния s и t имеют переходы по a в состояния из одной и той же группы в ?, заменить G в ?new на множество всех полученных подгрупп, }
(3) Если ?new = ?, полагаем ?res = ? и переходим к шагу 4, иначе повторяем шаг 2 с ? := ?new.
(4)

Таким образом, каждая группа в ?res становится состоянием нового автомата M'. Если группа содержит начальное состояние автомата M, то эта группа становится начальным состоянием автомата M'. Если группа содержит заключительное состояние M, она становится заключительным состоянием M'. Отметим, что каждая группа ?res либо состоит только из состояний из F, либо не имеет состояний из F. Переходы определяются очевидным образом.
(5) Если M' имеет "мертвое"состояние, то есть состояние, которое не является допускающим и из которого нет путей в допускающие, удалить его и связанные с ним переходы из M'. Удалить из M' также все состояния, недостижимые из начального.
Пример 3.10. Результат применения алгоритма 3.4 приведен на рис. 3.15.
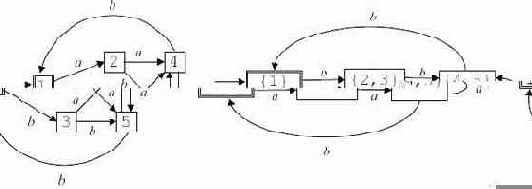
Рис. 3.15.