Теория и реализация языков программирования
Конечные автоматы
Регулярные выражения, введенные ранее, служат для описания регулярных множеств. Для распознавания регулярных множеств служат конечные автоматы. Недетерминированный конечный автомат (НКА) - по определению есть пятерка M = (Q, T, D, q0, F), где
- Q - конечное множество состояний,
- T - конечное множество допустимых входных символов (входной алфавит),
- D - функция переходов (отображающая множество во множество подмножеств множества Q), определяющая поведение управляющего устройства,

- - начальное состояние управляющего устройства,

- - множество заключительных состояний.

Работа конечного автомата представляет собой некоторую последовательность шагов, или тактов. Такт определяется текущим состоянием управляющего устройства и входным символом, обозреваемым в данный момент входной головкой. Сам шаг состоит из изменения состояния и, возможно, сдвига входной головки на одну ячейку вправо (рис. 3.2.).
Недетерминизм автомата заключается в том, что, во- первых, находясь в некотором состоянии и обозревая текущий символ, автомат может перейти в одно из, вообще говоря, нескольких возможных состояний, и во-вторых, автомат может делать переходы по e.
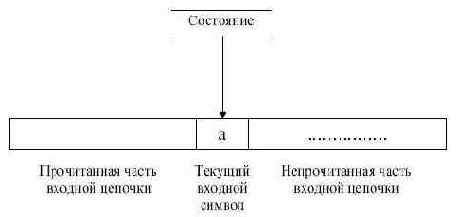
Рис. 3.2.
Пусть M = (Q, T, D, q0, F) - НКА. Конфигурацией автомата M называется пара






Будем обозначать символом





Важным частным случаем недетерминированного конечного автомата является детерминированный конечный автомат, который на каждом такте работы имеет возможность перейти не более чем в одно состояние и не может делать переходы по e.
Пусть M = (Q, T, D, q0, F) - НКА. Будем называть M детерминированным конечным автоматом (ДКА), если выполнены следующие два условия:
- D(q, e) = , для любого
 , и
, и
- D(q, a) содержит не более одного элемента для любых и
 .
.
Так как функция переходов ДКА содержит не более одного элемента для любой пары аргументов, для ДКА мы будем пользоваться записью D(q, a)=p вместо D(q, a)={p}.
Конечный автомат может быть изображен графически в виде диаграммы, представляющей собой ориентированный граф, в котором каждому состоянию соответствует вершина, а дуга, помеченная символом


Пример 3.3. Пусть L = L(r), где r = (a|b)*a(a|b)(a|b).
- Недетерминированный конечный автомат M, допускающий язык L:
M = {{1, 2, 3, 4}, {a, b}, D, 1, {4}},
где функция переходов D определяется так:
Диаграмма автомата приведена на рис. 3.3 а. - Детерминированный конечный автомат M, допускающий язык L:
M = {{1, 2, 3, 4, 5, 6, 7, 8}, {a, b}, D, 1, {3, 5, 6, 8}}
где функция переходов D определяется так:
Диаграмма автомата приведена на рис. 3.3 б.
- Недетерминированный конечный автомат M, допускающий язык L:
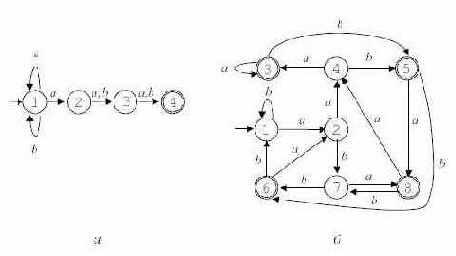
Рис. 3.3.
Пример 3.4. Диаграмма автомата, допускающего множество чисел в десятичной записи, приведена на рис. 3.4.
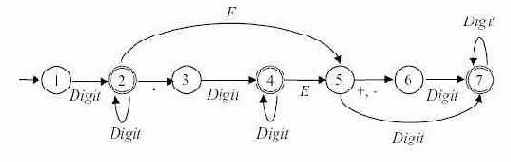
Рис. 3.4.
Пример 3.5. Анализ цепочек.
- При анализе цепочки w = ababa автомат из примера рис. 3.3, а, может сделать следующую последовательность тактов:

Состояние 4 является заключительным, отсюда, цепочка w допускается этим автоматом. - При анализе цепочки w = ababab автомат из примера рис. 3.3, б, должен сделать следующую последовательность тактов:

Так как состояние 7 не является заключительным, цепочка w не допускается этим автоматом.