MATLAB в инженерных и научных расчетах
Относительные значения граничных параметров при
|
№ п/п |
Граничные параметры рамы |
Относительные значения граничных параметров при критических силах |
||||
|
F1=15,098365 |
F2=30,980105 |
F3=73,913165 |
F4=132,291925 |
F5=212,607925 |
||
|
1 |
 |
-4.6771 |
24.7402 |
-6.2350 |
7.6095 |
-8.7618 |
|
2 |
 |
0.1771 |
-29.2402 |
1.7350 |
-12.1095 |
4.2618 |
|
3 |
 |
-8.0312 |
80.2205 |
-12.7049 |
28.8284 |
-20.2855 |
|
4 |
 |
1.0625 |
-175.4409 |
10.4098 |
-72.6569 |
25.5709 |
|
5 |
 |
6.0937 |
-258.6614 |
20.1147 |
-104.4853 |
42.8564 |
|
6 |
 |
-3.2651 |
-489.8187 |
-37.1538 |
-317.0371 |
-135.4205 |
|
7 |
 |
8.0312 |
-80.2205 |
12.7049 |
-28.8284 |
20.2855 |
|
8 |
 |
-2.7396 |
203,1811 |
-13.6448 |
83.2663 |
-31.3327 |
|
9 |
 |
6.0937 |
-258.6614 |
20.1147 |
-104.4853 |
42.8564 |
|
10 |
 |
8,0312 |
-80.2205 |
12.7049 |
-28.8284 |
20.2855 |
|
11 |
 |
-5.0312 |
83.2205 |
-9.7049 |
31.8284 |
-17.2855 |
|
12 |
 |
-0.6615 |
-15.3701 |
0.1175 |
-6.8047 |
1.3809 |
|
13 |
 |
3.3542 |
-55.4803 |
6.4699 |
-21.2190 |
11.5236 |
|
14 |
 |
-8.0312 |
80.2205 |
-12.7049 |
28.8284 |
-20.2855 |
|
15 |
 |
6.0937 |
-258.6614 |
20.1147 |
-104.4853 |
42.8564 |
|
16 |
 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
|
17 |
 |
-0.3542 |
58.4803 |
-3.4699 |
24.2190 |
-8.5236 |
|
18 |
 |
3.8021 |
-378.6220 |
24.0546 |
-155.9232 |
56.9037 |
|
19 |
 |
8.0312 |
-80.2205 |
12.7049 |
-28.8284 |
20.2855 |
|
20 |
 |
-5.0312 |
83.2205 |
-9.7049 |
31.8284 |
-17.2855 |
Формы потери устойчивости стержней рамы строятся по соотношениям метода начальных параметров. Для стержня 1-3 это выражение (3.26) продольно-поперечного изгиба, для остальных стержней – выражение (3.12) статического изгиба. Протокол построения форм потери устойчивости примет вид
x=0 : 0.001 : 1.0; f=15.098365; n2=sqrt(f);
EIV1=-(X(2,1)*x-X(4,1)*x.^3/6);
EIV2=-(X(17,1)*х-X(8,1)*x.^2/2-X(9,1)*x.^3/6);
EIV3=-(X(16,1)+X(12,1)*x-X(13,1)*x.^2/2-X(14,1)*x.*3/6);
EIV4=-(X(16,1)+X(17,1)*sin(n2*x)/n2-X(18,1)*(1-cos(n2*x))/n2^2- …
X(19,1)*(n2*x-sin(n2*x))/n2^3);
subplot
(2,2,1), plot (x, EIV1); axis
([0 1 - 0.1 0.1]); grid on
subplot
(2,2,2), plot (x, EIV2); axis
([0 1 - 0.1 0.1]); grid on
subplot
(2,2,3), plot (x, EIV3); axis
([0 1 - 1 1]); grid on
subplot (2,2,4), plot (x, EIV4); axis
([0 1 - 1 1]); grid on
Перед выполнением данного протокола в окно команд необходимо поместить вектор относительных граничных параметров Х при соответствующей критической силе Fi и не забывать корректировать масштабы форм потери устойчивости. Сами формы потери устойчивости представлены на рис. 3.21.
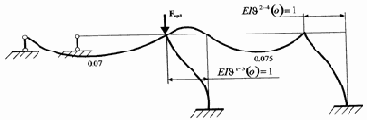 |
1-ая форма |
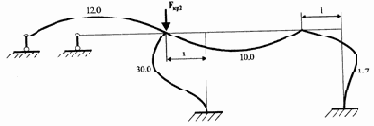 |
2-ая форма |
|
Рис. 3.21 |
|
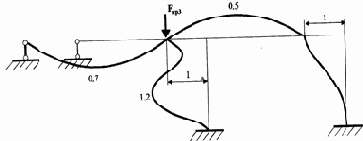 |
3-ая форма |
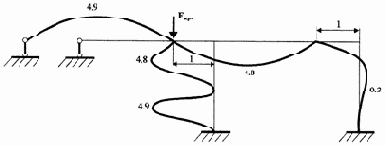 |
4-ая форма |
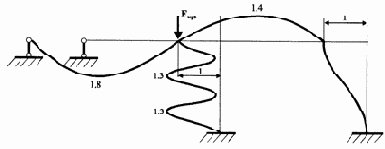 |
5-ая форма |
Окончание рис. 3.21
В заключение отметим еще одну замечательную особенность матрицы А* задач динамики и устойчивости. Эта матрица описывает связь между собой всех начальных и конечных параметров элементов упругой системы. Поэтому при поиске и построении форм собственных колебаний и потери устойчивости можно назначать единичное значение произвольному элементу матрицы нагрузки В. Последующая нормировка компонентов вектора Х*
относительно кинематических или статических параметров упругой системы приводит благодаря структуре матрицы А*
к одинаковым соотношениям между начальными и конечными граничными параметрами. Другими словами, значения относительных параметров таблиц 3.9, 3.7 и т. д. остаются неизменными независимо от положения единичного элемента матрицы В. Небольшие ограничения касаются тех элементов матрицы В, которые приводят к делению на ноль или

3.3.9. Построение эпюр напряженно-деформированного состояния
с разрывами 1-го рода
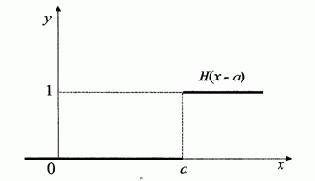
Примеры расчета неразрезной балки и рамы, приведенные в п. 3.1, 3.2, показывают, что необходимо учитывать разрывы 1-го рода при построении эпюр напряженно-деформированного состояния. Данная задача требует применения единичной функции Хевисайда Н(х-а) со сдвигом в точку а (рис. 3.22). В этом случае сокращаются тексты программ, а соответствующие эпюры можно получить сразу для всей длины стержня.
 |
 |
Рис. 3.22
В MATLAB нет встроенной единичной функции Хевисайда, поэтому ее необходимо программировать с применением операторов условного перехода if … end и логического оператора аnd. В качестве примера представим программу, позволяющую построить эпюры прогиба EIJ(x), угла поворота EIj(x), поперечных сил Q(x) и изгибающих моментов М(x) неразрезной балки по рис. 3.1, где выигрыш применения единичных функций наиболее очевиден. Для построения эпюр достаточно взять 500 – 600 точек. С учетом компонентов вектора Х формулы для параметров напряженно-деформированного состояния балки примут вид:
прогиб EIJ(x), 0 £ х £ 14.0 м.

Как видно из этого выражения необходимо применить 5 разных единичных функций. В формуле (3.36) разности в квадратных скобках представляют собой реакции опор 1, 2, 3.

Угол поворота EIj(x), 0 £ х £ 14.0 м.

Поперечная сила Q(x), 0 £ х £ 14.0 м.

Изгибающий момент М(x), 0 £ х £ 14.0 м.

Программа, реализующая формулы (3.36) – (3.39), организует цикл, в котором применен блок формирования единичных функций. Далее следуют операторы построения эпюр и вывод таблицы значений параметров напряженно-деформированного состояния всей балки. Здесь необходимо подставлять численные значения элементов вектора граничных параметров Х.
Текст программы
n=700; EIv=zeros(n,1); EIfi=zeros(n,1); Q=zeros(n,1);
M=zeros(n,1); x=0.0; dx=14.0/n; X=zeros(n,1);
for m = 1 : n
if and(x > = 0.0, x < = 2.0) h1=0; h2=0; h3=0; h4=0; h5=0; end;
if and(x > 2.0, x < = 4.0) h1=1; h2=0; h3=0; h4=0; h5=0; end;
if and(x > 4.0, x < = 10.0) h1=1; h2=1; h3=0; h4=0; h5=0; end;
if and(x > 10.0, x < = 12.0) h1=1; h2=1; h3=1; h4=0; h5=0; end;
if and(x > 12.0, x < = 13.0) h1=1; h2=1; h3=1; h4=1; h5=0; end;
if and(x > 13.0) h1=1; h2=1; h3=1; h4=1; h5=1; end;
EIv(m,1)= – (–12.79835*x – (–1.04938)*x.^3/6 + 10*(x – 2).^2*h1 + …
(–34.08093)*(x – 4).^3*h2/6 + 10*(x – 4).^4*h2/24 – …
10*(x – 10).^4*h3/24 + 4.36214*(x – 10).^3*h3/6 – …
40*(x – 12).^3*h4/6 + (–51.33059)*(x – 13).^3*h5/6);
EIfi(m,1)= – (–12.79835 – (–1.04938)*x.^2/2 + 20*(x – 2)*h1 + …
(–34.08093)*(x – 4).^2*h2/2 + 10*(x – 4).^3*h2/6 – …
10*(x – 10).^3*h3/6 + 4.36214*(x – 10).^2*h3/2 – …
20*(x – 12).^2*h4 + (–51.33059)*(x – 13).^2*h5/2);
Q(m,1)= (–1.04938) – (–34.08093)*h2 - 10*(x – 4)*h2 + …
10*(x – 10)*h3 - 4.36214*h3 + 40*h4 – …
(-
51.33059)*h5;
M(m,1)= (–1.04938)*x -
20*h1-(34.08093)*(x – 4)*h2 - …
- 5*(x – 4).^2*h2 + 5*(x – 10).^2*h3 - (4.36214)*(x – 10)*h3 + …
40*(x – 12)*h4 - (- 51.33059)*(x – 13)*h5; X(m,1)=x;
x = x + dx; end;
plot(X, EIv); grid on
% plot(X, Q); grid on
% plot(X, EIfi); grid on
% plot(X, M); grid on
[X EIv EIfi Q M]
На экране компьютера появится окно с первой эпюрой, совпадающей с рис. 3.1, затем, последовательно снимая символ комментария %, строятся другие эпюры, а в окно команд выводится таблица численных значений кинематических и статических параметров балки. Добавим, что совершенно аналогично можно строить эпюры с разрывами 1-го рода и для любых стержней рам. Если вместо оператора plot(X, EIv) использовать оператор stem(X, EIv,¢filled¢), то получится закрашенная эпюра, мало отличающаяся от обычного представления такого рода графиков. Можно сократить число используемых единичных функций до одной. Однако в этом случае единичную функцию необходимо создать в отдельном М-файле, например, такого содержания
function f = H(t)
if t < = 0.0 f = 0.0; else f = 1.0; end;
Этот файл должен быть записан в рабочей папке MATLAB (обычно это папка work) под именем Н. Тогда в головной программе построения эпюр можно использовать одну единичную функцию, но от разных аргументов, т.е.
Н(х – 2), Н(х – 4), Н(х – 10) и т.д. Например, выражение для прогиба (3.36) примет вид
EIv(m,1) = - (- 12.79835*x - (- 1.04938)*x.^3/6 + 10*(x – 2).^2*H(x – 2) + …
(-
34.08093)*(x – 4).^3*H(x – 4)/6 + 10*(x – 4).^4*H(x – 4)/24 - …
10*(x – 10).^4*H(x – 10)/24 + 4.36214*(x – 10).^3*H(x – 10)/6 - …
40*(x – 12).^3*H(x – 12)/6 - 51.33059*(x – 13).^3*H(x – 13)/6).
При выполнении программы на экране компьютера появляется эпюра по рис. 3.1. Аналогично программируются другие параметры.
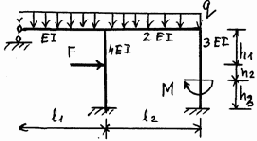
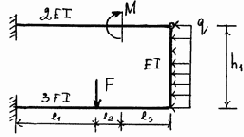
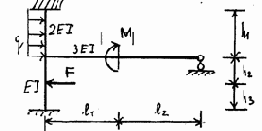
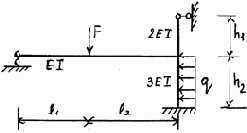
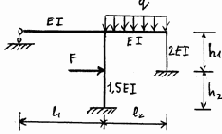
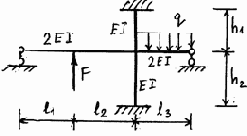
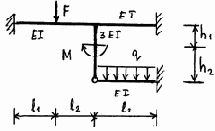
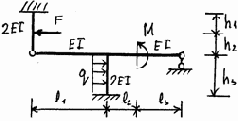
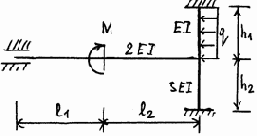
3.3.10. Варианты заданий
|
1 |
2 |
 |
 |
|
3 |
4 |
 |
 |
|
5 |
6 |
 |
 |
|
7 |
8 |
 |
 |
|
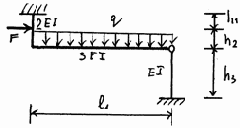
9 |
10 |
 |
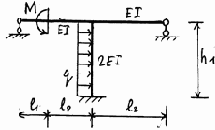 |
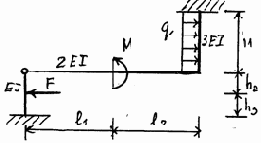
Рис. 3.23
|
11 |
12 |
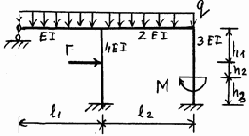 |
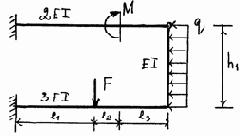 |
|
13 |
14 |
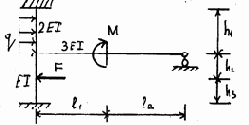 |
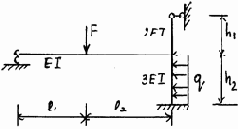 |
|
15 |
16 |
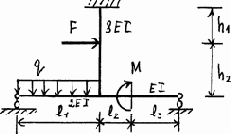 |
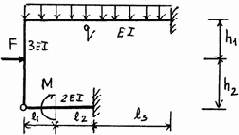 |
|
17 |
18 |
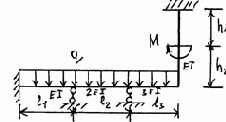 |
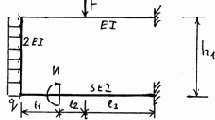 |
|
19 |
20 |
 |
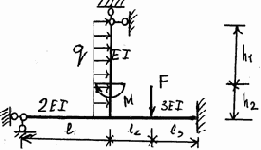 |
Продолжение рис. 3.23
|
21 |
22 |
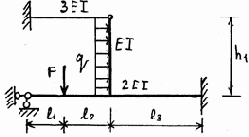 |
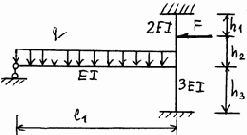 |
|
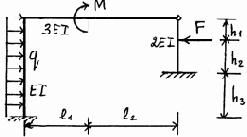
23 |
24 |
 |
 |
|
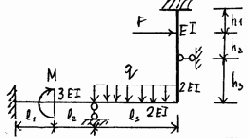
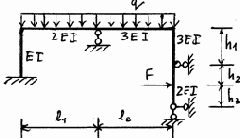
25 |
26 |
 |
 |
|
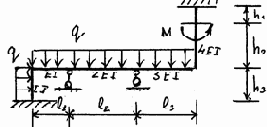
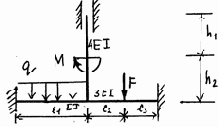
27 |
28 |
 |
 |
|
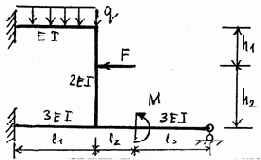
29 |
30 |
 |
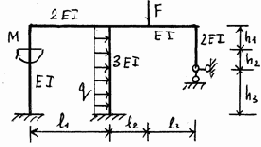 |
Окончание рис. 3.23
Таблица 3.10
Исходные данные к расчету плоских рам
|
№ варианта задания |
 |
 |
 |
h1 |
h2 |
h3 |
F |
M |
q |
|
м |
кН |
кНм |
кН/м |
||||||
|
1 |
1 |
3 |
4 |
2 |
3 |
4 |
10 |
16 |
10 |
|
2 |
2 |
3 |
5 |
3 |
1 |
2 |
40 |
12 |
8 |
|
3 |
3 |
4 |
2 |
2 |
1 |
2 |
5 |
20 |
6 |
|
4 |
5 |
4 |
1 |
2 |
1 |
2 |
25 |
25 |
4 |
|
5 |
5 |
1 |
3 |
3 |
4 |
4 |
10 |
15 |
2 |
|
6 |
2 |
6 |
4 |
2 |
2 |
1 |
10 |
15 |
12 |
|
7 |
1 |
3 |
3 |
2 |
1 |
2 |
30 |
40 |
20 |
|
8 |
1 |
3 |
1 |
1 |
2 |
1.5 |
60 |
15 |
15 |
|
9 |
3 |
4 |
6 |
1.5 |
2 |
3 |
30 |
25 |
12 |
|
10 |
4 |
2 |
3 |
4 |
2 |
1 |
28 |
40 |
8 |
|
11 |
1 |
1 |
2 |
1 |
2 |
2 |
12 |
15 |
6 |
|
12 |
4 |
5 |
4 |
1 |
2 |
3 |
5 |
40 |
10 |
|
13 |
2 |
3 |
4 |
2 |
1 |
1 |
3 |
15 |
18 |
|
14 |
2 |
1 |
1 |
2 |
4 |
3 |
40 |
20 |
10 |
|
15 |
5 |
2 |
4 |
4 |
3 |
2 |
15 |
15 |
5 |
|
16 |
1 |
3 |
2 |
4 |
5 |
1 |
20 |
6 |
12 |
|
17 |
5 |
4 |
2 |
3 |
2 |
2 |
40 |
10 |
10 |
|
18 |
1 |
2 |
1 |
4 |
3 |
1 |
25 |
20 |
8 |
|
19 |
3 |
1 |
4 |
2.5 |
4 |
5 |
25 |
25 |
14 |
|
20 |
5 |
4 |
1 |
2 |
4 |
5 |
15 |
16 |
12 |
|
21 |
1 |
2 |
3 |
5 |
4 |
3 |
10 |
15 |
16 |
|
22 |
4 |
2 |
4 |
3 |
2 |
1 |
30 |
40 |
22 |
|
23 |
5 |
4 |
2 |
4 |
4 |
2 |
60 |
18 |
17 |
|
24 |
1 |
3 |
5 |
2 |
4 |
5 |
30 |
25 |
14 |
|
25 |
4 |
2 |
2 |
1 |
2 |
4 |
28 |
40 |
10 |
|
26 |
5 |
3 |
2 |
2 |
2 |
1 |
20 |
18 |
6 |
|
27 |
3 |
2 |
1 |
2 |
3 |
4 |
25 |
40 |
10 |
|
28 |
5 |
4 |
4 |
2 |
3 |
4 |
20 |
15 |
18 |
|
29 |
2 |
3 |
1 |
3 |
4 |
5 |
40 |
20 |
10 |
|
30 |
1 |
2 |
5 |
4 |
5 |
1 |
15 |
15 |
7 |
Глава IV. Применение пакетов расширений МATLAB в
инженерно-научных задачах
4.1. Пакет расширений Symbolic Math
Система MATLAB является самой крупной системой компьютерной математики, ориентированной на матричные и численные вычисления. Однако MATLAB имеет также и средства аналитических вычислений. Пакет Symbolic Math Toolbox добавил системе MATLAB качественно новые возможности, связанные с выполнением символьных вычислений и преобразований, которые были доступны только в системе принципиально иного класса, относящихся к компьютерной алгебре. Теперь MATLAB, с учетом новых средств, становится в полной мере универсальной системой. Последняя реализация системы символьной математики Maple 6 в своем ядре и в расширениях имеет около 3000 функций. Система MATLAB с пакетом Symbolic, включающим в себя чуть больше сотни символьных команд и функций, намного уступает Maple по количеству таких команд и функций. Однако в данный пакет включены лишь наиболее важные и широко распространенные функции. Кроме того, есть специальная команда, которая дает доступ к ядру Maple, что заметно расширяет круг используемых функций.
Помимо типовых аналитических вычислений (таких как символьное дифференцирование и интегрирование, упрощение математических выражений, подстановка и т. д.) пакет Symbolic позволяет реализовать арифметические операции с произвольной точностью.