MATLAB в инженерных и научных расчетах
       

Относительные значения граничных



№ п/п
 Граничные
параметры рамы
 Относительные значения граничных параметров
 при собственных частотах


w1=2,946045
 w2=
9,431095
 w3=
13,959385
 w4=
15.259475
 w5=
19.489495
абсолютные
 относительные
1
= Х(1,1)=
 0.4361×107
 -5.3246
 -43.0898
 120.7308
 23.4396
 86.2844
2
=Х(2,1)=
 -0.0120×107
 0.1463
 8.0671
 43.7059
 -0.5996
 -6.7905
3
=Х(3,1)=
 0.8623×107
 -10.5288
 -155.6993
 531.9886
 110.7758
 449.5673
4
=Х(4,1)=
 -0.0763×107
 0.9316
 77.0857
 578.3407
 -8.6533
 -126.3574
5
=Х(5,1)=
 -0.4059×107
 4.9558
 77.7808
 81.0184
 -69.5101
 447.6958
6
=Х(6,1)=
 0.5355×107
 -6.5385
 50.4911
 -62.0186
 42.4069
 11.4058
7
=Х(7,1)=
 1.2201×107
 -14.9016
 220.3370
 -320.1960
 234.3273
 72.8153
8
=Х(8,1)=
 0.1871×107
 -2.2842
 -6.7060
 -65.7629
 -26.2838
 83.1398
9
=Х(9,1)=
 -0.4241×107
 5.1781
 -60.1557
 98.3542
 103.1128
 -443.2657
10
=Х(10,1)=
 -0.2047×107
 2.4991
 -120.4025
 420.3761
 8.3444
 241.4304
11
=Х(11,1)=
 0.3733×107
 -4.5580
 -10.8130
 -923.8486
 -90.5222
 604.9033
12
=Х(12,1)=
 0.0475×107
 -0.5802
 6.9230
 -12.0678
 -4.9911
 2.9949
13
=Х(13,1)=
 -0.2330×107
 2.8449
 3.4289
 63.5624
 0.6446
 90.1745
14
=Х(14,1)=
 0.2047×107
 -2.4991
 120.4025
 -420.3761
 -8.3444
 -241.4304
15
=Х(15,1)=
 -0.4059×107
 4.9558
 77.7808
 81.0184
 -69.5101
 447.6958
16
=Х(16,1)=
 -0.0819×107
 1.0000
 1.0000
 1.0000
 1.0000
 1.0000
17
=Х(17,1)=
 0.0227×107
 0.2776
 -8.6753
 -11.3875
 0.0157
 -4.4001
18
=Х(18,1)=
 -0.2514×107
 3.0696
 10.2235
 -112.4317
 29.4391
 -27.1176
19
=Х(19,1)=
 -0.2047×107
 2.4991
 -120.4025
 420.3761
 8.3444
 241.4304
20
=Х(20,1)=
 0.3733×107
 -4.5580
 -10.8130
 -923.8486
 -90.5222
 604.9033
<
Из таблицы следует, что единичные перемещения опор приводят к весьма значительным усилиям и перемещениям в элементах рамы.
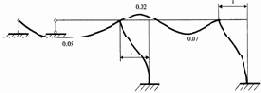
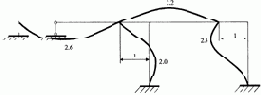
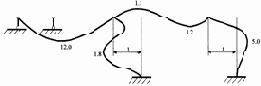
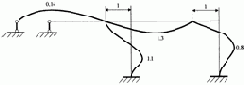
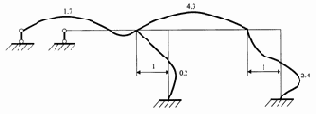
Формы колебаний стержней рамы, построенные по соотношениям метода начальных параметров (3.17) представлены на рис. 3.17. Протокол их построения запишется следующим образом.
Протокол построения форм колебаний принимает вид
х = 0 : 0.001 : 1.0;  у = 2.946045; la1 = sqrt (у); la2 = sqrt (у);
la3 = (2*у^2)^0.25; la4 = (4*у^2)^0.25;
EIv1 = - (X(2,1)*(sinh(la1*x)+sin(la1*x))/(2*
la1) - X(4,1)*(sinh(la1*x) - …
sin(la1*x))/(2*
la1^3));
EIv2 = - (X(17,1)*(sinh(la2*x)+sin(la2*x))/(2*
la2) - X(8,1)*(cosh(la2*x) - …
cos(la2*x))/(2*
la2^2) - X(9,1)*(sinh(la2*x)-sin(la2*x))/(2*
la2^3));
EIv3 = - (X(16,1)*(cosh(la3*x)+cos(la2*x))/2+ X(12,1)*(sinh(la3*x)+ …
sin(la3*x))/(2*
la3) - X(13,1)* (cosh(la3*x)-cos(la*x))/(2* la3^2) - …
X(14,1)*(sinh(la3*x)-sin(la3*x))/(2*
la3^3));
Eiv4 = - (X(16,1)*(cosh(la4*x)+cos(la4*x))/2 + X(17,1)*(sinh(la4*x) + …
sin(la4*x))/(2*la4) -
X(18,1)*(cosh(la4*x)-cos(la4*x))/(2* la4^2) - …
X(19,1)*(sinh(la4*x)-sin(la4*x))/(2*
la4^3));
subplot (2,2,1), plot (x, EIv1); axis
([0 1 - 0.1  0.1]); grid on
subplot (2,2,2), plot (x, EIv2); axis
([0 1 - 0.1  0.1]); grid on
subplot (2,2,3), plot (x, EIv3); axis
([0 1  -   1     1]); grid on
subplot (2,2,4), plot (x, EIv4); axis
([0 1  -   1     1]); grid on
Как и при расчете неразрезной балки, перед выполнением данного протокола в окно команд помещается вектор относительных граничных параметров Х, также необходимо корректировать масштабы форм колебаний.

1 форма

2 форма



3 форма

4 форма


5 форма

Содержание раздела