MATLAB в инженерных и научных расчетах
Расчет на вынужденные колебания
Отметим, что данный расчет спектра частот и форм собственных колебаний кинематическим способом является основой расчета
сооружений на сейсмические воздействия. Можно заключить, что представленная методика по МГЭ является наиболее простой и эффективной по сравнению с имеющимися [3].
3.3.5. Расчет на вынужденные колебания
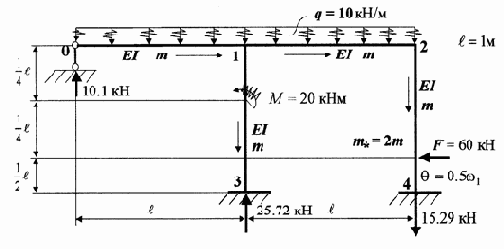 |
b(3,1)= q*(cosh (la1) -cos(la1))/(2*la1^2);
b(4,1)= q*(sinh (la1)+ sin(la1))/(2*la1);
a(6,17)=(sinh(la2)+sin(la2))/(2*la2); a(6,8) = - (cosh(la2) - cos(la2))/(2*la2^2);
a(6,9)=-(sinh(la2)-sin(la2))/(2*la2^3); a(7,17)=(cosh(la2)+cos(la2))/2;
a(7,8) =- a(6,17); a(7,9) =
a(6,8); a(7,12) = - 1; a(8,13) = - 1;
a(8,17) = la2^4*a(6,9); a(8,8) = a(7,17); a(8,9) =
a(6,17); a(9,15) = - 1;
a(9,17) = la2^4*a(6,8); a(9,8) =- a(8,17); a(9,9) =
a(7,17); a(10,14) = 1;
a(10,10) = 1; b(6,1)= - q*(cosh (la2)+cos(la2) -2)/(2*la2^4);
b(7,1)= - q*(sinh (la2)- sin(la2))/(2*la2^3);
b(8,1)= q*(cosh (la2) -cos(la2))/(2*la2^2);
b(9,1)= q*(sinh (la2)+ sin(la2))/(2*la2);
a(11,12)=(sinh(la3)+sin(la3))/(2*la3); a(11,13)=-(cosh(la3)-cos(la3))/(2*la3^2);
a(11,14)=-(sinh(la3)-sin(la3))/(2*la3^3); a(11,16)=(cosh(la3)+cos(la3))/2;
a(12,12)=a(11,16); a(12,13)=-a(11,12); a(12,14)=a(11,13); a(12,16)=-la3^4*a(11,14);
a(13,1)=-1; a(13,12)=- a(12,16); a(13,13)=a(11,16); a(13,14)=a(11,12);
a(13,16)= la3^4*a(11,13);
a(14,12)=a(13,16); a(14,13)=a(12,16);
a(14,14)=a(11,16); a(14,3)=-1; a(14,16)=la3^4*a(12,13);
a(15,5) =-1; a(15,15)=1; b(11,1)=-f*(sinh (la3/2)- sin(la3/2))/(2*la3^3);
b(12,1)= - f*(cosh (la3/2) -cos(la3/2) -2)/(2*la3^2);
b(13,1)= f*(sinh (la3/2)+ sin(la3/2))/(2*la3);
b(14,1)= f*(cosh (la3/2) + cos(la3/2))/2;
a(16,16)=(cosh(la4)+cos(la4))/2; a(16,17)=(sinh(la4)+sin(la4))/(2*la4);
a(16,18)=-(cosh(la4)-cos(la4))/(2*la4^2); a(16,19)=-(sinh(la4)-sin(la4))/(2*la4^3);
a(17,16)=- la4^4*a(16,19); a(17,17)=a(16,16);
a(17,18)=-a(16,17); a(17,19)=a(16,18);
a(18,6)=-1; a(18,16)=la4^4*a(16,18); a(18,17)=-a(16,17); a(18,18)=a(16,16);
a(18,19)=a(16,17); a(19,7) = - 1; a(19,16)=-la4^4*a(17,18);
a(19,17)=a(18,16);
a(19,18)=a(17,16); a(19,19)=a(16,16); a(20,11) = - 1; a(20,20) = 1;
b(16,1)= - m*(cosh (3*la4/4) -cos(3*la4/4))/(2*la4^2);
b(17,1)=-m*(sinh (3*la4/4) +
sin(3*la4/4))/(2*la4);
b(18,1)= m*(cosh (3*la4/4) + cos(3*la4/4))/2;
b(19,1)= m*(la4sinh (3*la4/4) - sin(3*la4/4))/2;
X = a\ b
Результаты расчета динамических граничных параметров рамы сведены в таблицу 3.8.