MATLAB в инженерных и научных расчетах
solid windowtext
|
12. |
xi |
-25.0 |
-23.0 |
-21.0 |
-18.0 |
-17.2 |
-15.4 |
-14.0 |
||||||||||
|
yi |
0.76 |
0.74 |
0.61 |
0.58 |
0.84 |
0.92 |
1.22 |
|||||||||||
|
13. |
xi |
-4.0 |
-3.0 |
-2.0 |
-1.0 |
0.0 |
1.0 |
2.0 |
||||||||||
|
yi |
1.71 |
1.56 |
1.24 |
1.36 |
1.78 |
2.21 |
4.31 |
|||||||||||
|
14. |
xi |
-22.0 |
-20.0 |
-18.0 |
-16.0 |
-14.0 |
-12.0 |
-10.0 |
||||||||||
|
yi |
-2.26 |
-1.84 |
-1.92 |
-1.76 |
-1.56 |
-1.64 |
-1.34 |
|||||||||||
|
15. |
xi |
23.0 |
24.0 |
25.0 |
26.0 |
27.0 |
28.0 |
29.0 |
||||||||||
|
yi |
1.26 |
1.37 |
1.44 |
1.56 |
1.15 |
1.28 |
1.06 |
|||||||||||
|
16. |
xi |
30.0 |
33.0 |
35.0 |
37.0 |
39.0 |
41.0 |
43.0 |
||||||||||
|
yi |
-2.6 |
-3.7 |
-2.5 |
-4.3 |
-2.3 |
-5.6 |
-1.9 |
|||||||||||
|
17. |
xi |
44.0 |
45.0 |
46.0 |
47.0 |
48.0 |
49.0 |
50.0 |
||||||||||
|
yi |
2.24 |
3.46 |
5.36 |
1.89 |
1.76 |
1.54 |
2.12 |
|||||||||||
|
18. |
xi |
52.0 |
54.0 |
56.0 |
58.0 |
60.0 |
62.0 |
64.0 |
||||||||||
|
yi |
-1.28 |
-1.33 |
-1.44 |
-1.67 |
-1.77 |
-2.81 |
-2.16 |
|||||||||||
|
19. |
xi |
2.2 |
2.6 |
3.0 |
3.4 |
3.8 |
4.2 |
4.6 |
||||||||||
|
yi |
1.88 |
1.65 |
1.61 |
1.73 |
1.56 |
1.24 |
1.99 |
|||||||||||
|
20. |
xi |
5.1 |
5.3 |
5.5 |
5.7 |
5.9 |
6.1 |
6.3 |
||||||||||
|
yi |
-2.8 |
-3.6 |
-5.7 |
-3.4 |
-1.9 |
-1.7 |
-1.5 |
|||||||||||
|
21. |
xi |
7.15 |
7.35 |
7.55 |
7.75 |
7.95 |
8.15 |
8.35 |
||||||||||
|
yi |
-2.2 |
-3.6 |
-1.7 |
-2.8 |
-1.6 |
-4.5 |
-2.2 |
|||||||||||
|
22. |
xi |
9.1 |
9.2 |
9.3 |
9.4 |
9.5 |
9.6 |
9.7 |
||||||||||
|
yi |
1.48 |
1.16 |
2.08 |
1.96 |
1.81 |
2.31 |
5.61 |
|||||||||||
|
23. |
xi |
-10.2 |
-10.1 |
-10.0 |
-9.9 |
-9.8 |
-9.7 |
-9.6 |
||||||||||
|
yi |
-6.5 |
-7.8 |
-10.2 |
-5.4 |
-4.6 |
-9.5 |
-10.3 |
|||||||||||
|
24. |
xi |
11.0 |
14.0 |
17.0 |
20.0 |
23.0 |
26.0 |
29.0 |
||||||||||
|
yi |
1.2 |
1.6 |
1.9 |
1.1 |
1.16 |
1.24 |
1.36 |
|||||||||||
|
25. |
xi |
-50.0 |
-48.0 |
-46.0 |
-44.0 |
-42.0 |
-40.0 |
-38.0 |
||||||||||
|
yi |
1.23 |
1.32 |
1.57 |
1.19 |
1.16 |
1.10 |
2.28 |
|||||||||||
|
26. |
xi |
-36.0 |
-34.0 |
-32.0 |
-30.0 |
-28.0 |
-26.0 |
-24.0 |
||||||||||
|
yi |
1.1 |
1.3 |
2.1 |
1.9 |
1.7 |
1.5 |
1.8 |
|||||||||||
|
27. |
xi |
21.0 |
23.0 |
24.0 |
28.0 |
31.0 |
32.0 |
36.0 |
||||||||||
|
yi |
1.24 |
1.37 |
1.56 |
1.64 |
1.84 |
1.26 |
1.14 |
|||||||||||
|
28. |
xi |
10.0 |
13.0 |
17.0 |
22.0 |
28.0 |
35.0 |
43.0 |
||||||||||
|
yi |
1.21 |
1.36 |
1.51 |
1.84 |
1.06 |
1.21 |
1.36 |
|||||||||||
|
29. |
xi |
-1.0 |
0.0 |
3.0 |
5.0 |
8.0 |
12.0 |
15.0 |
||||||||||
|
yi |
-2.1 |
-3.6 |
1.2 |
-4.3 |
1.8 |
2.6 |
-0.2 |
|||||||||||
|
30. |
xi |
-8.0 |
-7.0 |
-5.0 |
-3.0 |
-1.0 |
2.0 |
5.0 |
||||||||||
|
yi |
1.36 |
1.88 |
2.45 |
-2.1 |
-10.2 |
-4.4 |
1.16 |
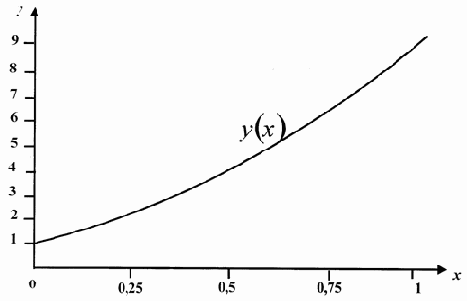 |
Таблица 2.4
|
хi |
Метод Рунге-Кутта |
Точное решение |
|
0.0 |
1.0 |
1.0 |
|
0.1 |
1.2221 |
1.2221 |
|
0.2 |
1.4977 |
1.4977 |
|
0.3 |
1.8432 |
1.8432 |
|
0.4 |
2.2783 |
2.2783 |
|
0.5 |
2.8274 |
2.8274 |
|
0.6 |
3.5202 |
3.5202 |
|
0.7 |
4.3928 |
4.3928 |
|
0.8 |
5.4895 |
5.4895 |
|
0.9 |
6.8645 |
6.8645 |
|
1.0 |
8.5836 |
8.5836 |
/p> Как следует из таблицы 2.4 численное решение программой ode45 является точным.
Варианты заданий. Построить график и вывести в виде таблицы решение задачи Коши на интервале [0; 1] методом Рунге-Кутта 4-го порядка. Данные взять из таблицы 2.5.
Таблица 2.5
|
№ п/п |
f(x,y) |
y0 |
|
1. |
 |
0.0 |
|
2. |
 |
0.1 |
|
3. |
 |
2.0 |
|
4. |
 |
0.3 |
|
5. |
 |
0.4 |
|
6. |
 |
0.0 |
|
7. |
 |
0.1 |
|
8. |
 |
0.2 |
|
9. |
 |
0.3 |
|
10. |
 |
0.4 |
|
11. |
 |
0.5 |
|
12. |
 |
0.0 |
|
13. |
 |
0.5 |
|
14. |
 |
0.4 |
|
15. |
 |
0.3 |
|
16. |
 |
0.2 |
|
17. |
 |
0.1 |
|
18. |
 |
0.0 |
|
19. |
 |
0.1 |
|
20. |
 |
0.2 |
|
21. |
 |
0.3 |
|
22. |
 |
0.4 |
|
23. |
 |
0.5 |
|
24. |
 |
0.6 |
|
25. |
 |
0.7 |
|
26. |
 |
0.0 |
|
27. |
 |
0.1 |
|
28. |
 |
0.2 |
|
29. |
 |
0.3 |
|
30. |
 |
0.4 |
/p> 2.5. Приближенное вычисление определенных интегралов
К вычислениям определенных интегралов сводятся многие практические задачи физики, химии, экологии, механики и других естественных наук. На практике формулой Ньютона-Лейбница не всегда удается воспользоваться. В этом случае используются методы численного интегрирования. Они основаны на следующих соображениях: с геометрической точки зрения определенный интеграл

Метод трапеций.
Здесь используется линейная аппроксимация, т. е. график функции y = f(x) представляется в виде ломаной, соединяющей точки yi. Формула трапеций при постоянном шаге


В MATLAB данную формулу реализует программа trapz (x,y).
Метод Симпсона
Если подынтегральную функцию заменить параболой, то формула Симпсона с постоянным шагом интегрирования предстанет в виде

В MATLAB формула Симпсона реализуется программой quad. Подынтегральная функция может задаваться с помощью дескриптора @, тогда она программируется в файле – функции, или с помощью апострофов, тогда она записывается в самой программе quad. Точность вычисления интегралов по умолчанию принята равной 1×10-6.
Пример 6. Вычислить и вывести на печать по методам трапеций и Симпсона значения интеграла

Протокол программы метода трапеций
>> x
= 0 : 0.0001 : 1.0 ;
>> y
= 1./ (1+x.^2) ;
>> z
= trapz(x, y)
Результат вычислений
z =
0.7854
Протокол программы метода Симпсона
>> quad ( ¢ (1./(1+x.^2)) ¢, 0, 1)
Результат вычислений
ans =
0.7854
Точное значение интеграла равно 0.785398163.
Как видно из примера 6 полученные результаты являются практически точными, а сами протоколы весьма просты.
Варианты заданий. Вычислить и вывести на печать значения определенного интеграла методами трапеций и Симпсона. Данные взять из таблицы 2.6.
Таблица 2.6
|
№ п/п |
Подынтегральная функция f(x) |
Интервал интегрирования [a; b] |
Точность вычислений интеграла |
|
1 |
 |
[1; 3.5] |
0.001 |
|
2 |
 |
[p/6; [p/3] |
0.002 |
|
3 |
 |
[1.5; 3.] |
0.0001 |
|
4 |
 |
[1.0; 4,0] |
0.003 |
|
5 |
 |
[0; ln2] |
0.0015 |
|
6 |
 |
[1.0; 4.0] |
0.002 |
|
7 |
 |
[0.0; 2.0] |
0.001 |
|
8 |
 |
[2.0; 5.0] |
0.001 |
|
9 |
 |
[1.0; 2.5] |
0.0005 |
|
10 |
 |
[0.0;  |
0.003 |
|
11 |
 |
[0.0; 3,0] |
0.001 |
|
12 |
 |
[1.5; 3.0] |
0.0025 |
|
13 |
 |
[0,0; 5.0] |
0.001 |
|
14 |
 |
[2.3; 6.0] |
0.002 |
|
15 |
 |
[0.0; p/2] |
0.001 |
|
16 |
 |
[0.0; 2.0] |
0.0015 |
|
17 |
 |
[0.0; 2.0] |
0.002 |
|
18 |
 |
[0.0; p/4] |
0.001 |
|
19 |
 |
[0.0; 1.8] |
0.0006 |
|
20 |
 |
[0.0; p] |
0.0016 |
|
21 |
 |
[0.0; 1.2] |
0.002 |
|
22 |
 |
[2.0; 4.4] |
0.0014 |
|
23 |
 |
[0.0; 1.2] |
0.002 |
|
24 |
 |
[2.0; 4.4] |
0.0011 |
|
25 |
 |
[1.0; 2.2] |
0.0023 |
|
26 |
 |
[0,0; 1.8] |
0.0015 |
|
27 |
 |
[0.0; 1.2] |
0.001 |
|
28 |
 |
[1.0; 3.0] |
0.002 |
|
29 |
 |
[0.0; 1.0] |
0.0013 |
|
30 |
 |
[1.0; 2.2] |
0.0025 |
Задача нахождения корней нелинейных уравнений встречается в различных областях научно-технических исследований. Проблема формулируется следующим образом. Пусть задана непрерывная функция f(x) и требуется найти корень уравнения
f(x) = 0.
Будем предполагать, что имеется интервал изменения х [a; b], на котором необходимо исследовать функцию f(x) и найти значение х0, при котором f(x0) равно или весьма мало отличается от нуля.
Данная задача в системе MATLAB может быть решена следующим образом. Вначале необходимо построить график функции f(x) на заданном интервале и убедиться в существовании корня или нескольких корней. Затем применить программы поиска корней. Если существует один корень и график f(x) пересекает ось ох, то можно применить программу fzero. Если f(x) имеет больше одного корня и может касаться и пересекать ось ох, то следует применить более мощную программу fsolve из пакета Optimization Toolbox, которая решает задачу методом наименьших квадратов. Программа fzero использует известные численные методы: деление отрезка пополам, секущей и обратной квадратичной интерполяции.
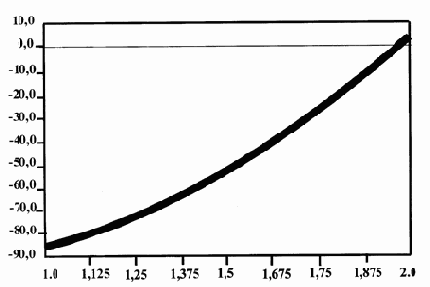
Пример 7. Найти корень нелинейного уравнения 10х + 2х – 100 = 0 на интервале [1.0; 2.0].
Протокол программы
>> % Строим график заданной функции
>> x
= 1.0 : 0.001 : 2.0; y = 10.0.^x + 2.0*x
– 100.0;
>> рlot
(x, y) ; grid on
Появляется окно с графиком функции 10х + 2х – 100 (см. рис. 2.4), из которого следует, что корень функции на заданном интервале существует. Для точного определения корня применяем fzero и fsolve.
 |
>> X1 = fzero
( ¢ (10.0.^x
+ 2.0*x – 100.0) ¢, [1.0 2.0])
Результат решения
Х1 =
1.9824
>> X2 =
fsolve ( ¢ (10.0.^x
+ 2.0*x – 100.0) ¢, 1.0 : 2.0)
Результат решения
Х2 =
1.9824 1.9824
Варианты заданий. Построить график и найти корень нелинейного уравнения. Данные взять из таблицы 2.7.
Таблица 2.7
|
№ п/п |
Уравнение f(x) = 0 |
Отрезок [a; b] |
|
1 |
 |
[1.0;  |
|
2 |
 |
[2.0; 3.0] |
|
3 |
 |
[8.0; 9.0] |
|
4 |
 |
[0.5; 1.0] |
|
5 |
 |
[0.0; 1.0] |
|
6 |
 |
[3.0; 3.2] |
|
7 |
 |
[0.0; 1.0] |
|
8 |
 |
[0.0; 0.2] |
|
9 |
 |
[0.8; 1.0] |
|
10 |
 |
[2.6; 3.0] |
|
11 |
 |
[1.0; 1.5] |
|
12 |
 |
[1.0; 2.0] |
|
13 |
 |
[0.0; 1.0] |
|
14 |
 |
[0.0; 1.0] |
|
15 |
 |
[3.0; 4.0] |
|
16 |
 |
[1.0; 1.2] |
|
17 |
 |
[1.0; 2.0] |
|
18 |
 |
[0.0; 1.0] |
|
19 |
 |
[-0.2; -0.1] |
|
20 |
 |
[0.1; 0.9] |
|
21 |
 |
[1.0; 1.4] |
|
22 |
 |
[3.0; 4.0] |
|
23 |
 |
[0.0; 1.5] |
|
24 |
 |
[0.0; 1.0] |
|
25 |
 |
[0.1; 1.0] |
|
26 |
 |
[0.4; 0.6] |
|
27 |
 |
[3.0; 4.0] |
|
28 |
 |
[4.0; 5.0] |
|
29 |
 |
[2.0; 3.0] |
|
30 |
 |
[0.0; 0.48] |
/p> 2.7. Численное решение оптимизационных задач
Под оптимизацией понимают процесс выбора наилучшего варианта из всех возможных. С точки зрения инженерных расчетов методы оптимизации позволяют выбрать наилучший вариант конструкции, наилучшее распределение ресурсов, минимальный урон природной среде и т. п. В процессе решения задачи оптимизации необходимо найти оптимальные значения некоторых параметров, их называют проектными параметрами. Выбор оптимального решения проводится с помощью некоторой функции, называемой целевой функцией. Целевую функцию можно записать в виде

где х1, х2, … , хп – проектные параметры.
Можно выделить 2 типа задач оптимизации – безусловные
и условные. Безусловная задача оптимизации состоит в отыскании максимума или минимума функции (2.10) от п действительных переменных и определении соответствующих значений аргументов на некотором множестве G n-мерного пространства. Обычно рассматриваются задачи минимизации; к ним легко сводятся и задачи на поиск максимума путем замены знака целевой функции на противоположный. Условные задачи оптимизации – это такие, при формулировке которых задаются некоторые условия (ограничения) на множестве G. Здесь рассмотрим только безусловные задачи оптимизации.
Поиск минимума функции одной переменной.
Для решения этой задачи используются методы золотого сечения или параболической интерполяции (в зависимости от формы задания функции), реализованные в программе fminbnd.
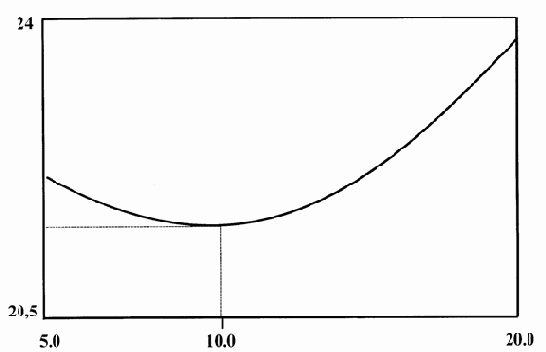
Пример 8. Найти и вывести на печать минимальное значение функции
f(x) = 24 – 2x /3 + x2/ 30 на [5; 20].
Строим график этой функции, чтобы убедиться в наличии минимума на заданном интервале.
Протокол программы
>> x = 5.0 : 0.001 : 20.0 ; y = 24 – 2* x/3 + x.^2/30 ;
>> рlot(x, y) ; grid on
Появляется окно с графиком этой функции (рис. 2.5), где отмечаем наличие минимума.
 |
Далее, для точного определения координаты и значения минимума привлекаем программу fminbnd.
>> [x, y] = fminbnd ( ¢ (24.0 – 2* x/3 + x.^2/30) ¢, 5.0, 20.0)
Результат поиска
х
=
10.0000
у
=
20.6667
Варианты заданий. Найти и вывести на печать координату и минимальное значение функции f(x) на [a; b]. Данные взять из таблицы 2.8.
Таблица 2.8
|
№ п/п |
Функция f(x) |
Отрезок [a; b] |
|
1 |
 |
[1.2; 4] |
|
2 |
 |
[0; p/2] |
|
3 |
 |
[-2; 2] |
|
4 |
 |
[-2; 2] |
|
5 |
 |
[1; 3] |
|
6 |
 |
[p; 3p/2] |
|
7 |
 |
[0; 1] |
|
8 |
 |
[0; 2] |
|
9 |
 |
[-0.5; 1.5] |
|
10 |
 |
[0,1; 1.0] |
|
11 |
 |
[-0.5; 0,5] |
|
12 |
 |
[-1.0; 0] |
|
13 |
 |
[-0.5; 0.5] |
|
14 |
 |
[0.5; 1.5] |
|
15 |
 |
[1.6; 2.2] |
|
16 |
 |
[1; 2] |
|
17 |
 |
[1.1; 1.6] |
|
18 |
 |
[0; p/3] |
|
19 |
 |
[0.5; 1.2] |
|
20 |
 |
[-1.5; -0.5] |
|
21 |
 |
[-2.0; -1.0] |
|
22 |
 |
[-2.0; -1.0] |
|
23 |
 |
[0.1; 1.0] |
|
24 |
 |
[-0,05; -0.2] |
|
25 |
 |
[-0.5; 0.5] |
|
26 |
 |
[p; 3p/2] |
|
27 |
 |
[1.0; 2.0] |
|
28 |
 |
[0.1; 0.5] |
|
29 |
 |
[p; 2p] |
|
30 |
 |
[2.0; 3.0] |
Поиск минимума функций нескольких переменных
Данная задача значительно сложнее первой. Рассмотрим ее решение на примере функции двух переменных. Алгоритм может быть распространен на функции большего числа переменных. Для минимизации функций нескольких переменных MATLAB использует симплекс – метод Нелдера-Мида. Данный метод является одним из лучших методов поиска минимума функций многих переменных, где не вычисляются производные или градиент функции. Он сводится к построению симплекса в п-мерном пространстве, заданного п + 1 вершиной. В двухмерном пространстве симплекс является треугольником, а в трехмерном – пирамидой. На каждом шаге итераций выбирается новая точка решения внутри или вблизи симплекса. Она сравнивается с одной из вершин симплекса. Ближайшая к этой точке вершина симплекса заменяется этой точкой. Таким образом, симплекс перестраивается и позволяет найти новое, более точное положение точки решения. Алгоритм поиска повторяется, пока размеры симплекса по всем переменным не станет меньше заданной погрешности решения. Программу, реализующую симплекс-методы Нелдера-Мида, удобно использовать в следующей записи
[x, min f] = f min search ( … ),
где х – вектор координат локального минимума;
min f – значение целевой функции в точке минимума.
Саму целевую функцию удобно представить с помощью дескриптора @ в М-файле.
Пример 9. Найти и вывести на печать координаты и значение минимума функции двух переменных f(x, y) = (x2 + y2 – 3)2 + (x2 + y2 – 2x – 3)2 + 1, если начальная точка поиска имеет координаты М0 (1; 1). Анализ функции показывает, что min f = 1 x = 0,

Строим трехмерный график этой функции, чтобы убедиться в наличии минимума. Возьмем интервал х є [-1; 1]; y є [1; 3].
Протокол программы
>> [X,Y] = mesh grid ( [-1 : 1, 1 : 3] ) ;
>> Z = (X.^2 + Y.^2 – 3).^2 + (X.^2 + Y.^2 – 2*X – 3).^2 + 1 ;
>> рlot 3 (X,Y,Z)
После построения трехмерного графика выполняем поиск минимума. В М-файле программируем целевую функцию
function f = F xy(x)
f = (x(1) ^ 2 + x(2) ^ 2 –3)^2 – 3)^2 + (x(1) ^ 2 + x(2) ^ 2 –2* x(1) – 3)^2 + 1;
Решаем поставленную задачу в окне команд
>> [xmin, mi f] = fminsearch ( @ Fxy, [1; 1] )
Результаты поиска
xmin =
- 0.0000 1.7320
minf =
1.0000
Как видно, результаты решения задачи точные.
Варианты заданий. Найти и вывести на печать координаты и минимальное значение функции двух переменных. Поиск начать с точки М0 (х0, у0). Данные взять из таблицы 2.9.
Таблица 2.9
|
№ п/п |
Функция f(x, у) |
Координаты начальной точки М0 (х0, у0). |
|
1 |
2 |
3 |
|
1 |
 |
(1; 1) |
|
2 |
 |
(2; 2) |
|
3 |
 |
(2; 2) |
|
4 |
 |
(2; 2) |
|
5 |
 |
(2; 2) |
|
6 |
 |
(2; 2) |
|
7 |
 |
(2; 2) |
|
8 |
 |
(2; 2) |
|
9 |
 |
(2; 2) |
|
1 |
2 |
3 |
|
10 |
 |
(2; 2) |
|
11 |
 |
(0.5; 0.5) |
|
12 |
 |
(0.5; 3.5) |
|
13 |
 |
(0; 0) |
|
14 |
 |
(0.1; -1.0) |
|
15 |
 |
(4; 1) |
|
16 |
 |
(0.5; 2.5) |
|
17 |
 |
(1.5; 0.5) |
|
18 |
 |
(0.5; 0.5) |
|
19 |
 |
(0.3; 0.3) |
|
20 |
 |
(0.25; 0.25) |
|
21 |
 |
(0.5; 1.5) |
|
22 |
 |
(0.5; 0.5) |
|
23 |
 |
(-1.5; 0.5) |
|
24 |
 |
(1.0; 1.0) |
|
25 |
 |
(2.0; 1.5) |
|
26 |
 |
(0.2; 0.3) |
|
27 |
 |
(p/4; p/4) |
|
28 |
 |
(p/4; p/4) |
|
29 |
 |
(2.5; 2.5) |
|
30 |
 |
(1.0; -1.0) |
/p> В заключение отметим, что представленные примеры использования возможностей MATLAB в решении различных научно-технических проблем являются лишь небольшой иллюстрацией значительно большего потенциала системы, а материал главы может служить некоторым введением при самостоятельном изучении и применении интегрированного пакета математического моделирования. Следующая глава ориентирована на решение в среде MATLAB прикладных задач сугубо инженерной науки – строительной механики, где нашли свое применение отдельные вопросы численных методов.
ГЛАВА 3. Применение MATLAB для решения задач
строительной механики стержневых систем
Изложенные выше основные данные о программировании и использовании численных методов в интегрированном пакете математического моделирования MATLAB показывают его большие возможности в решении задач прикладных наук. Одной из наиболее значимых прикладных наук в механико-инженерном образовании является строительная механика, где рассматриваются вопросы расчета машиностроительных, судостроительных, авиационных, строительных и т. п. конструкций. Объединение в одном пакете программирования и визуализации результатов расчетов позволяет существенно обогатить учебный процесс, повысить его методический уровень и наглядность теории, значительно уменьшить время на выполнение индивидуальных заданий и обеспечить глубокое овладение современными компьютерными технологиями. По этим причинам внедрение MATLAB в учебный процесс является актуальной задачей высшей школы. Важным условием высокого научного уровня учебного процесса является также широкое использование современных достижений соответствующих наук. В частности, в строительной механике накоплен большой арсенал методов расчета стержневых конструкций на статическую, динамическую нагрузки и устойчивость. Одним из наиболее эффективных методов строительной механики является метод граничных элементов (МГЭ), разработанный рядом зарубежных и отечественных ученых. В данной книге применен численно-аналитический вариант МГЭ, который с исчерпывающей полнотой изложен в работе [2]. Как ниже будет показано, реализация МГЭ в пакете MATLAB исключает какое-либо программирование численных процессов. Сами программы представляют собой лишь процесс введения исходных матриц и вызов численных процедур, т. е. реализуются в полном объеме идеи структурного программирования, что значительно уменьшает количество ошибок и повышает достоверность результатов. Дальнейшая графическая визуализация результатов расчетов логически завершает постановку задачи и ее решение. Таким образом, объединение современных достижений науки и компьютерных технологий будет способствовать подготовке высококвалифицированных специалистов и магистров. Кратко рассмотрим суть МГЭ в задачах деформирования стержневых систем.
3. 1 Основные положения метода граничных элементов
Значительное число задач механики упругого стержня сводится к решению линейного неоднородного дифференциального уравнения с постоянными коэффициентами

удовлетворяющего начальным условиям

Как известно, такая задача определения частного решения уравнения (3.1), удовлетворяющего условием (3.2), называется задачей Коши. Для изгиба, поперечных колебаний, кручения тонкостенных стержней, продольно-поперечного изгиба и т. п. видов деформирования, решение задачи Коши можно записать в матричной форме.
|
EIn(x) |
= |
A11 |
A12 |
-A13 |
-A14 |
|
EIn(o) |
+  |
A14(x-x) |
q(x)dx , |
(3.3) |
|
EIj(x) |
A21 |
A22 |
-A23 |
-A24 |
|
EIj(o) |
A24(x-x) |
||||
|
M(x) |
-A31 |
-A32 |
A33 |
A34 |
|
M(o) |
-A34(x-x) |
||||
|
Q(x) |
-A41 |
-A42 |
A43 |
A44 |
|
Q(o) |
-A44(x-x) |
Y(x) = A(x) X(o) + B(x), (3.4)
где Y(x) – вектор параметров напряженно-деформированного состояния стержня в текущей точке;
A(x) – квадратная матрица фундаментальных ортонормированных функций уравнения (3.1);
X(o) – вектор начальных параметров;
B – вектор (матрица-столбец) внешней нагрузки.
Если несколько стержней соединены в единую конструкцию, то для системы стержней можно составить матричное уравнение типа (3.4). Матрица А преобразуется к квазидиагональному виду, а векторы Y, X и B будут содержать параметры состояния всех стержней по следующей структуре
|
А= |
А1 |
|
|
|
|
; Y = |
Y1 |
; X = |
X1 |
; B = |
B1 |
(3.5) |
|
|
А2 |
|
|
|
Y2 |
X2 |
B2 |
|||||
|
|
|
O |
|
|
M |
M |
M |
|||||
|
|
|
|
Аn-1 |
|
Yn-1 |
Xn-1 |
Bn-1 |
|||||
|
|
|
|
|
Аn |
Yn |
Xn |
Bn |
/p> Если координате х каждого стержня дать граничное значение

Y











где конечные граничные параметры матрицы Y переносятся на место нулевых параметров вектора Х. При этом, эти векторы дополняются уравнениями равновесия и совместности перемещений узловых точек и граничными условиями. В конце схемы преобразований (3.6) получается система линейных алгебраических уравнений относительно начальных и конечных параметров всех стержней конструкции. После вычисления начальных параметров стержней их напряженно-деформированное состояние определяется по матричному уравнению (3.3). Таким образом, решение прямых задач строительной механики стержневых систем в МГЭ сводится к решению одной системы линейных алгебраических уравнений и вычислению напряженно-деформированного состояния в промежуточных точках по соотношениям метода начальных параметров. Такая схема решения обеспечивает получение весьма точных и достоверных результатов, которые можно представить средствами MATLAB в виде обычных эпюр, форм свободных колебаний, потерь устойчивости и т. п.
Главной операцией в схеме (3.6) является перенос параметров из Y в X. Процесс переноса конечных параметров вектора Y в вектор X основан на следующих положениях. Векторы Y, X любой стержневой (и не стержневой) конструкции при граничном значении координаты

Первая группа – это нулевые граничные параметры, что определяется заданными условиями опирания (краевыми условиями).
Вторая группа – это зависимые параметры, связанные между собой обычными уравнениями равновесия и совместности перемещений узлов конструкции.
Третья группа граничных параметров никак не связаны между собой. Эти параметры условно могут быть названы независимыми. Перенос параметров из вектора Y в вектор X должен компенсироваться ненулевыми элементами матрицы А, иначе нарушается исходное уравнение схемы (3.6). Очевидно, что независимые параметры вектора Y должны быть перенесены на место нулевых параметров вектора X, а зависимые параметры переносятся в соответствии с уравнениями их связи. Перед операцией переноса параметров необходимо освободить поля матрицы А
от элементов, связанных с нулевыми параметрами вектора Х, т. е. обнулить столбцы матрицы А, номера которых равны номерам нулевых строк матрицы Х. Далее в матрицу А вводятся ненулевые компенсирующие элементы и преобразования по схеме (3.6) завершены, поскольку в матрице В изменяются только знаки элементов. Правило для определения величины и положения компенсирующих элементов при переносе параметров включает 3 основных случая.
1-й случай. При переносе независимого параметра вектора Y в вектор X компенсирующий элемент матрицы А равен коэффициенту при переносимом параметре со своим знаком по схеме
|
|
i |
j |
k |
l |
|
|
- |
|
|
(3.7) , |
  |
|
 |
 |
 |
Xi1=0;Yk1 |
i |
Yi1=0 |
|||
|
j |
|
1 |
 |
 |
Xj1 |
j |
Yj1=0 |
|||
 |
-a |
|
1 |
 |
Xk1 |
k |
аYk1 |
|||
|
l |
|
|
|
1 |
Xl1 |
l |
Yl1=0 |
2-й случай. Перенос зависимых параметров представляет собой повторение операцией 1-го случая с той лишь разницей, что в матрице Х не появляются новые параметры, а в матрице А* соответствующие строки могут содержать несколько компенсирующих элементов
|
|
i |
j |
k |
l |
|
|
- |
|
|
(3.8) . |
  |
-a |
b |
|
|
Xi1= 0;Yl1 |
i |
Yi1 = aYl1 - bХj1 |
|||
|
j |
|
|
|
|
Xj1 |
j |
Yj1 = 0 |
|||
|
k |
|
|
|
|
Xk1 |
k |
Yk1 = 0 |
|||
|
l |
-1 |
|
|
|
Xl1 |
l |
Yl1 |
/p> 3-й случай. В сложных конструкциях в одном узле могут находиться несколько начальных точек стержней. В этом случае возникают уравнения связи между начальными параметрами и требуется переносить параметры в пределах вектора Х. Компенсирующие элементы в этом случае формируются из системы фундаментальных функций, столбцы которой получают сдвиг в соответствии со схемой
 |
|
|
i |
j |
k |
l |
|
|
; |
|
  |
1 |
 |
 |
 |
Xi1 |
|||
|
j |
|
1 |
 |
 |
Xj1 |
|||
 |
|
|
1 |
 |
Xk1=а Xi1 |
|||
|
l |
|
|
|
1 |
Xl1 |
|
|
i |
j |
k |
l |
|
|
|
|
i |
1 |
 |
|
 |
Xi1 |
|
|
|
j |
-al |
1 |
|
 |
Xj1 |
|
|
|
k |
a |
|
|
 |
|
|
|
|
l |
|
|
|
1 |
Xl1 |
. |
Видно, что элементы матрицы А сдвигаются на место столбца, номер которого равен номеру строки нового положения параметра. Компенсирующие элементы равны произведению коэффициента при переносимом параметре на элементы матрицы А. При этом возрастает число компенсирующих элементов по сравнению со случаями 1 и 2. Поэтому необходимо, по возможности, избегать случаев, когда в узле сходятся только начальные точки стержней.
Более подробно алгоритм формирования системы линейных алгебраических уравнений типа (3.6) для стержневых систем рассмотрен ниже, при решении конкретных задач.
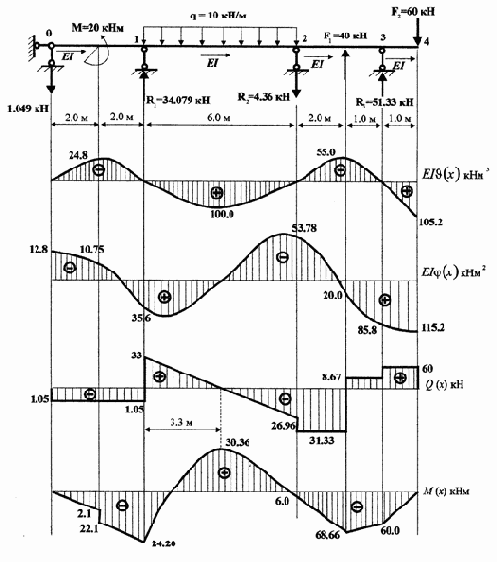
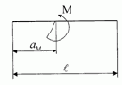
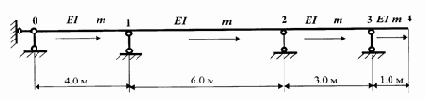
3.2. Расчет неразрезной балки
 |
 |
 |
 |
||||
|
b(1,1) = |
-M* (l – am)^2/2; |
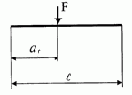
b(1,1) = |
-F* (l –af)^3/6; |
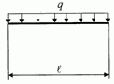
b(1,1) = |
-q*l^4/24; |
(3.10) |
|
b(2,1) = |
-M* (l – am); |
b(2,1) = |
-F* (l –af)^2/2; |
b(2,1) = |
-q*l^3/6; |
|
|
b(3,1) = |
M; |
b(3,1) = |
F* (l –af); |
b(3,1) = |
q*l^2/2; |
|
|
b(4,1) = |
O; |
b(4,1) = |
F |
b(4,1) = |
q*l. |
/p> Рис. 3.2
3.2.1. Определение граничных параметров при статической
нагрузке
Исходные данные расчета балки:
l1 = 4.0; l2
= 6.0; l3 = 3.0; l4 = 1.0; m = 20.0; q
= 10.0; f1 = - 40.0; f2 = 60.0; am = 2.0; af1
= 2.0; af2 = 1.0.
Система линейных уравнений для граничных параметров балки
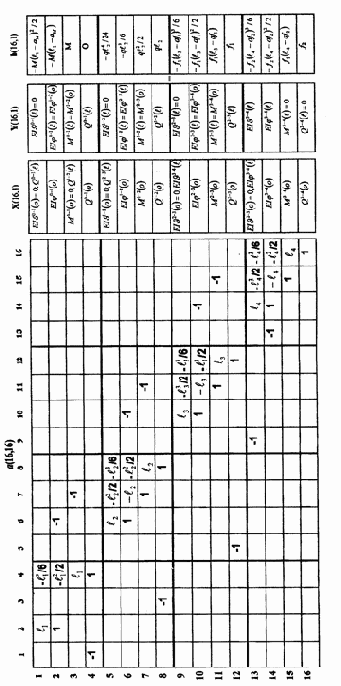 |
(3.11) |
Протокол с комментариями
|
% Описание матрицы а(16,16); b(16,1) и Х(16,1); |
|
а = zeros(16,16); ); b = zeros (16,1); Х = zeros (16,1); |
|
% Исходные данные расчета балки |
|
l1 = 4.0; l2 = 6.0; l3 = 3.0; l4 = 1.0; m = 20.0; q = 10.0; |
|
f1 = - 40.0; f2 = 60.0; am = 2.0; af1 = 2.0; af2 = 1.0; |
|
% Ввод матриц а(16,16) и b(16,1) с помощью операторов присваивания; |
|
a(1,2) = l1; a(1,4) = -l1^3/6; b(1,1) = -m*(l1-am)^2/2; |
|
a(2,2) = 1.0; a(2,4) = -l1^2/2; a(2,6) = -1.0; b(2,1) = -m*(l1-am); |
|
a(3,4) = l1; a(3,7) = -1.0; b(3,1) = m; a(4,1) = -1.0; a(4,4) = 1.0; |
|
a(5,6) = l2; a(5,7) = -l2^2/2; a(5,8) = -l2^3/6; b(5,1) = -q*l2 ^4/24; |
|
a(6,6) = 1.0; a(6,7) = -l2; a(6,8) = -l2^2/2; a(6,10) = -1.0; |
|
b(6,1) = -q*l2 ^3/6; a(7,7) = 1.0; a(7,8) = l2; a(7,11) = -1.0; |
|
b(7,1) = q*l2^2/2; a(8,3) = -1.0; a(8,8) = 1.0; b(8,1) = q*l2; |
|
a(9,10) = l3; a(9,11) = -l3^2/2; a(9,12) = -l3^3/6; |
|
b(9,1) = -f1*(l3-af1)^3/6; a(10,10) = 1.0; a(10,11) = -l3; |
|
a(10,12) = -l1^2/2; a(10,14) = -1.0; b(10,1) = -f1*(l3-af1)^2/2; |
|
a(11,11) = 1.0; a(11,12) = l3; a(11,15) = -1.0; b(11,1) = f1*(l3-af1); |
|
a(12,5) = -1.0; a(12,12) = 1.0; ; b(12,1) = f1; a(13,9) = -1.0; |
|
a(13,14) = l4; a(13,15) = -l4^2/2; a(13,16) = -l4^3/6; |
|
b(13,1) = -f2*(l4-af2)^3/6; a(14,13) = -1.0; a(14,14) = 1.0; |
|
a(14,15) = -l4; a(14,16) = -l4^2/2; b(14,1) = -f2*(l4-af2)^2/2; |
|
a(15,15) = -1.0; a(15,16) = l4; b(15,1) = f2*(l4-af2); a(16,16) = 1.0; |
|
b(16,1) = f2; |
|
% Решение системы уравнений ах = b и вывод результатов |
|
Х = a\ b |
/p> Результаты вычисления граничных параметров представлены в таблице 3.1.
Таблица 3.1
|
1 |
 |
9 |
 |
|
2 |
 |
10 |
 |
|
3 |
 |
11 |
 |
|
4 |
 |
12 |
 |
|
5 |
 |
13 |
 |
|
6 |
 |
14 |
 |
|
7 |
 |
15 |
 |
|
8 |
 |
16 |
 |
для исключения нулевых ведущих элементов, что является дополнительным преимуществом MATLAB по сравнению с непосредственным программированием метода исключения Гаусса в таких средах, как Delphi, Visual Fortran, Visual C++ и т.п.
3.2.2. Построение эпюр прогибов, углов поворота, поперечных сил
и изгибающих моментов
Эпюры параметров изгиба можно строить для каждого стержня в отдельности, используя соотношения метода начальных параметров. При этом удобно выполнять построение эпюр в одном окне, для чего можно привлекать процедуру subplot. Для соблюдения требуемого масштаба можно использовать процедуру axis. Масштабная сетка эпюр появится, если задействовать процедуру grid on. Выполнение этих требований приводит к следующим операторам построения эпюр
subplot (2, 2, 1), plot (x, EIn); axis ( [0 2 -150 150] ); grid on
subplot (2, 2, 2), plot (x, EIfi); axis ( [0 2 -150 150] ); grid on
subplot (2, 2, 3), plot (x, Q); axis ( [0 2 -100 100] ); grid on
subplot (2, 2, 4), plot (x, M); axis ( [0 2 -100 100] ); grid on.
Протокол построения эпюр удобно поместить в отдельный М-файл и по мере необходимости корректировать масштаб изображения графиков. Выражения для параметров изгиба стержня по методу начальных параметров имеют вид

где элементы от внешней нагрузки запишутся следующим образом:

Положительные направления внешней нагрузки и их координаты показаны на рис. 3.3
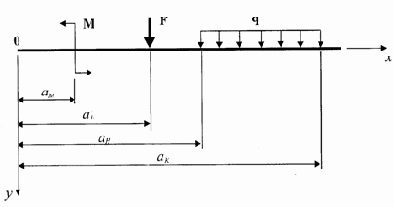 |
Для балки по рис. 3.1 протоколы построения эпюр примут вид:
Стержень 0 – 1
x = 0 : 0.001 : 2.0;
EIn
= - (X(2,1).* – X(4,1).*x.^3/6);
EIfi
= - (X(2,1) – X(4,1).*x.^2/2);
Q = X(4,1); M = X(4,1).*x;
subplot (2, 2, 1), plot (x, EIn); axis ( [0 2 -150 150] ); grid on
subplot (2, 2, 2), plot (x, EIfi); axis ( [0 2 -150 150] ); grid on
subplot (2, 2, 3), plot (x, Q); axis ( [0 2 -100 100] ); grid on
subplot (2, 2, 4), plot (x, M); axis ( [0 2 -100 100] ); grid on.
После построения графиков ( нажатия кнопки ВЫПОЛНИТЬ) необходимо продолжить формирование команд для завершения эпюр на интервале (2; 4) в М-файле
x = 2.0 : 0.001 : 4.0; m = 20.0;
EIn = - (X(2,1).* – X(4,1).*x.^3/6 + m.*(x – 2).^2/2);
EIfi
= - (X(2,1) – X(4,1).*x.^2/2 + m.*(x – 2));
Q = X(4,1); M = X(4,1).*x – m;
subplot (2, 2, 1), plot (x, EIn); axis ( [2 4 -150 150] ); grid on
subplot (2, 2, 2), plot (x, EIfi); axis ( [2 4 -150 150] ); grid on
subplot (2, 2, 3), plot (x, Q); axis ( [2 4 -100 100] ); grid on
subplot (2, 2, 4), plot (x, M); axis ( [2 4 -100 100] ); grid on.
Стержень 1 – 2
x = 0 : 0.001 : 6.0; q = 10.0;
EIn = - (X(6,1).*x – X(7,1).*x.^2/2 – X(8,1).*x.^3/6 + q.*x.^4/24);
EIfi
= - (X(6,1) – X(7,1).*x – X(8.1).*x.^2/2 + q.*x.^3/6);
Q = X(8,1) – q.*x; M = X(7,1) + X(8,1).*x – q.*x.^2/2;
subplot (2, 2, 1), plot (x, EIn); axis ( [0 6 -150 150] ); grid on
subplot (2, 2, 2), plot (x, EIfi); axis ( [0 6 -150 150] ); grid on
subplot (2, 2, 3), plot (x, Q); axis ( [0 6 -100 100] ); grid on
subplot (2, 2, 4), plot (x, M); axis ( [0 6 -100 100] ); grid on.
Стержень 2 – 3
x = 0 : 0.001 : 2.0;
EIn
= - (X(10,1).*x – X(11,1).*x.^2/2 – X(12,1).*x.^3/6);
EIfi
= - (X(10,1) – X(11,1).*x – X(12,1).*x.^2/2);
Q = X(12,1); M = X(11,1) + X(12,1).*x;
subplot (2, 2, 1), plot (x, EIn); axis ( [0 2 -150 150] ); grid on
subplot (2, 2, 2), plot (x, EIfi); axis ( [0 2 -150 150] ); grid on
subplot (2, 2, 3), plot (x, Q); axis ( [0 2 -100 100] ); grid on
subplot (2, 2, 4), plot (x, M); axis ( [0 2 -100 100] ); grid on.
Далее вторая часть эпюр строится по операторам
x =2. 0 : 0.001 : 3.0;
EIn
= - (X(10,1).*х – X(11,1).*x.^2/2 – X(12,1).*x.^3/6 – f1.*(x –2).^3/6);
EIfi
= - (X(10,1) – X(11,1).*x – X(12,1).*x.^2/2 – f1.*(x –2).^2/2);
Q = X(12,1) + f1; M = X(11,1) + X(12,1).*x + f1.*(x –2);
subplot (2, 2, 1), plot (x, EIn); axis ( [2 3 -150 150] ); grid on
subplot (2, 2, 2), plot (x, EIfi); axis ( [2 3 -150 150] ); grid on
subplot (2, 2, 3), plot (x, Q); axis ( [2 3 -100 100] ); grid on
subplot (2, 2, 4), plot (x, M); axis ( [2 3 -100 100] ); grid on
Стержень 3 – 4
x = 0 : 0.001 : 1;
EIn
= - (X(14,1).*x – X(15,1).*x.^2/2 – X(16,1).*x.^3/6);
EIfi
= - (X(14,1) – X(15,1).*x– X(16,1).*x.^2/2);
Q = X(16,1); M = X(15,1) + X(16,1).*x;
subplot (2, 2, 1), plot (x, EIn); axis ( [0 1 -150 150] ); grid on
subplot (2, 2, 2), plot (x, EIfi); axis ( [0 1 -150 150] ); grid on
subplot (2, 2, 3), plot (x, Q); axis ( [0 1 -100 100] ); grid on
subplot (2, 2, 4), plot (x, M); axis ( [0 1 -100 100] ); grid on.
Следует помнить, что в окно команд необходимо вводить значения неизвестных начальных параметров балки, т. е. вектор Х. Это легко выполняется с помощью отдельного М-файла, на котором записана процедура решения матричного уравнения неразрезной балки. После вектора Х нужно ввести также значения внешней нагрузки и их координаты. Эпюры EIn(х), EIj(х), Q(х) и М(х) представлены на рис. 3.1.
3.2.3. Определение частот собственных колебаний
 |
Исходные данные:

Матрица фундаментальных функций поперечных колебаний
|
; |
 |
(3.14) |
|||||
|
Аi = |
A11 |
A12 |
-A13 |
-A14 |
|||
|
l4A14 |
A11 |
-A12 |
-A13 |
||||
|
-l4A13 |
-l4A14 |
A11 |
A12 |
||||
|
-l4A12 |
-l4A13 |
l4A14 |
A11 |
||||
çА*(w) ç= 0,
где матрица А*(w) берется из задачи статики с заменой матриц фундаментальных функций изгиба на матрицы функций поперечных колебаний
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
/p>
| 3-4 |
| 2-3 |
| 1-2 |
| 0-1 |
выводятся на печать в формате long e. При просмотре таблицы их значений определяются точки, где определитель изменяет знак. Эти точки и будут являться частотами собственных колебаний. Иногда бывают случаи, когда график функции d = çА*(w) çкасается оси w. Для контроля этих точек полезно построить график у
= d(w), просмотр которого позволяет определить интервалы, где находятся корни и существуют ли точки касания графика оси w. Далее корни могут быть уточнены повторными прогонами программы (без построения графика у = d(w). Рекомендуется начинать поиск корней с начального значения частоты


Обозначения переменных, принятых в программе
а - матрица А*(w); п – порядок матрицы А*(w); п1
– число циклов вычисления определителя çА*(w)ç; аm
– частота собственных колебаний; dam
– шаг изменения частоты w; m – счетчик цикла вычисления определителя; l1, l2, l3, l4 – длины стержней неразрезной балки; lа – коэффициент l фундаментальных функций; Х – вектор значений частоты w; Y – вектор значений определителя çА*(w)ç.
Текст программы
l1 = 4.0; l2 = 6.0; l3 = 3.0; l4 = 1.0; n = 16; n1 = 300; am = 0,01;
dam = 0.01; X = zeros (n1,1); Y = zeros (n1,1);
for m = 1 : n1
la = sqrt (am); a
= zeros (n,n);
a(1,2) = (sinh(la*l1) + sin (la*l1))/(2*la);
a(1,4) = - (si h(la*l1) - sin (la*l1))/(2*la^3);
a(2,2)=(cosh(la*l1)+cos(la*l1))/2; a(2,4) = - (cos h(la*l1) - cos (la*l1))/(2*la^2);
a(2,6) = - 1; a(3,2) = la^ 4*a(1,4); a(3,4) = a(1,2); a(3,7) = - 1; a(4,1) = - 1;
a(4,2) = la^ 4*a(2,4); a(4,4) = a(2,2);
a(5,6) = (sinh(la*l2) + sin (la*l2))/(2*la);
a(5,7)= - (cosh(la*l2) -cos(la*l2))/(2*la^2);
a(5,8) = - (sinh(la*l2) - sin (la*l2))/(2*la^ 3);
a(6,6)=(cosh(la*l2)+cos(la*l2))/2; a(6,7) = - a(5,6); a(6,8) = a(5,7);
a(6,10) = - 1; a(7,6) = la^ 4*a(5,8); a(7,7) = a(6,6); a(7,8) = a(5,6); a(7,11) = - 1;
a(8,3) = - 1; a(8,6) = la^ 4*a(5,7); a(8,7) = - a(7,6); a(8,8) = a(6,6);
a(9,10) = (sinh(la*l3) + sin (la*l3))/(2*la);
a(9,11)= - (cosh(la*l3) -cos(la*l3))/(2*la^2);
a(9,12) = - (sinh(la*l3) - sin (la*l3))/(2*la^ 3);
a(10,10)=(cosh(la*l3)+cos(la*l3))/2; a(10,11) = - a(9,10); a(10,12) = a(9,11);
a(10,14) = - 1; a(11,10) = la^ 4*a(9,12); a(11,11) = a(10,10); a(11,12) = a(9,10);
a(11,15) = - 1; a(12,5) = - 1; a(12,10) = la^ 4*a(9,11); a(12,11) = - a(11,10);
a(12,12) = a(10,10); a(13,9) = - 1; a(13,14) = (sin h(la*l4) + sin (la*l4))/(2*la);
a(13,15)= - (cosh(la*l4) -cos(la*l4))/(2*la^2);
a(13,16) = - (sinh(la*l4) - sin (la*l4))/(2*la^ 3); a(14,13) = - 1;
a(14,14)=(cosh(la*l4)+cos(la*l4))/2; a(15,14) = la^ 4*a(13,16);
a(15,15) = a(14,14); a(15,16)=
a(13,14); a(16,14) = la^ 4*a(13,15);
a(16,15) = - a(15,14);
a(16,16) = a(14,16);
d = det(a); X(m,1) = am; Y(m,1) = d; am = am + dam; end;
% Построение графика у
= d(am)
plot (X,Y); grid оn
% Вывод на печать таблицы значений am и d
format long e
[X Y]
График определителя d = êA*(w) êдля балки принимает вид (рис. 3.5)
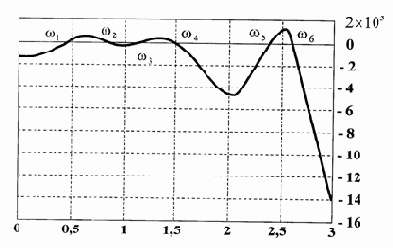 |
Как следует из рис. 3.5, график определителя d = êA*(w) ê не имеет точек разрыва 2-го рода (это большое преимущество метода граничных элементов), не касается оси w
и имеет точки пересечения с горизонталью. Эти точки отмечены символами w1, w2
и т. д. Уточнение частот приводит к следующим значениям

и т. д.
3.2.4. Построение форм собственных колебаний
Для построения форм собственных колебаний необходимо определить граничные параметры стержней балки. Эта задача может быть решена следующим образом:
1. Используется статический или кинематический способ возбуждения собственных колебаний. Для этого приравнивается единице
статический или кинематический параметр матрицы Y(


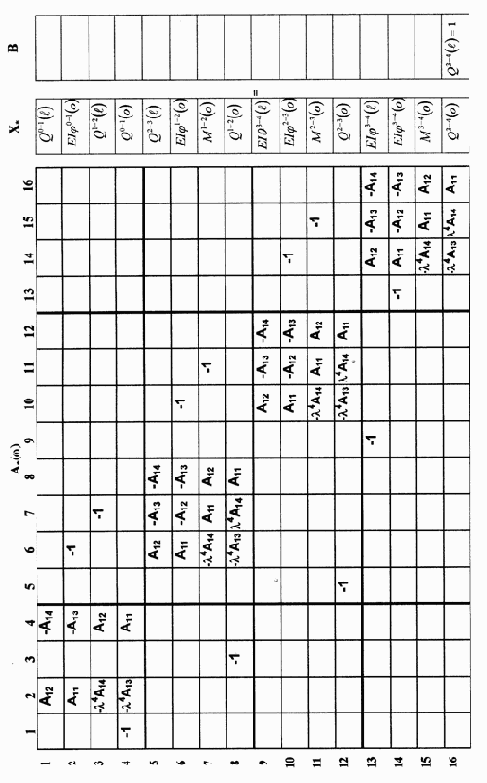 |
(3.16) |
EIn3-4(

2. По нормированным начальным параметрам строятся формы собственных колебаний балки средствами MATLAB.
Уравнение для граничных параметров балки отличается от уравнения (3.11) только фундаментальными функциями и вектором правой части (см. (3.16)).
Программа вычисления граничных параметров набирается в отдельном М-файле и принимает вид
a = zeros (16,16); b =
zeros (16,1); X = zeros
(16,1); la = sqrt (0,4055125);
l1 = 4.0; l2 =
6.0; l3 = 3.0; l4 = 1.0;
a(1,2) = (sinh(la*l1) + sin (la*l1))/(2*la);
a(1,4) = - (sinh(la*l1) - sin (la*l1))/(2*la^3);
a(2,2)=(cosh(la*l1)+cos(la*l1))/2; a(2,4) = - (cosh(la*l1) - cos (la*l1))/(2*la^2);
a(2,6) = - 1; a(3,2) = la^ 4*a(1,4); a(3,4) = a(1,2); a(3,7) = - 1; a(4,1) = - 1;
a(4,2) = la^ 4*a(2,4); a(4,4) = a(2,2); a(5,6) = (sinh(la*l2) + sin (la*l2))/(2*la);
a(5,7)= - (cosh(la*l2) - cos(la*l2))/(2*la^2);
a(5,8) = - (sinh(la*l2) - sin (la*l2))/(2*la^ 3);
a(6,6)=(cosh(la*l2)+cos(la*l2))/2;
a(6,7) = -a(5,6); a(6,8) =a(5,7);
a(6,10) = -1; a(7,6) =la^ 4*a(5,8); a(7,7) =a(6,6);
a(7,8) = a(5,6); a(7,11) = - 1; a(8,3) = - 1; a(8,6) = la^ 4*a(5,7); a(8,7) = - a(7,6);
a(8,8) = a(6,6); a(9,10) = (sinh(la*l3) + sin (la*l3))/(2*la);
a(9,11)= - (cosh(la*l3) -cos(la*l3))/(2*la^2);
a(9,12) =-(sinh(la*l3)-sin(la*l3))/(2*la^3);
a(10,10)=(cosh(la*l3)+cos(la*l3))/2;
a(10,11) = - a(9,10); a(10,12) = a(9,11); a(10,14) = - 1; a(11,10) = la^ 4*a(9,12);
a(11,11) =a(10,10); a(11,12)= a(9,10); a(11,15)= -1; a(12,5)= -1; a(12,11) = - a(11,10);
a(12,10)=la^ 4*a(9,11); a(12,12)=a(10,10);
a(13,14)=(sinh(la*l4) + sin (la*l4))/(2*la);
a(13,9) = - 1; a(13,15)= - (cos h(la*l4) -cos(la*l4))/(2*la^2);
a(13,16) = - (sinh(la*l4) - sin (la*l4))/(2*la^ 3); a(14,13) = - 1;
a(14,14)=(cosh(la*l4)+cos(la*l4))/2; a(14,15) = - a(13,14); a(14,16) =
a(13,15);
a(15,14) = la^ 4*a(13,16); a(15,15) = a(14,14);
a(15,16) = a(13,14); a(16,14) = la^ 4*a(13,15);
a(16,15) = - a(15,14); a(16,16) = a(14,14); b(16,1) = 1; X = a\ b;
X = X \ X(9,1)
Результаты вычислений относительных значений граничных параметров балки при собственных частотах сведены в таблицу 3.2.
Таблица 3.2
|
№ п/п |
Граничные параметры балки |
Относительные значения граничных параметров при частотах |
||||
|
w1=0,4055125 |
w2=0,7818475 |
w3=1,1001125 |
w4=1,4852935 |
w5=2,4234325 |
||
|
1 |
 |
0.1677 |
- 3.5779 |
0.3375 |
- 0.4569 |
- 0.9724 |
|
2 |
 |
- 1.4419 |
3.5754 |
- 0.2308 |
0.3784 |
- 0.4260 |
|
3 |
 |
- 1.6643 |
- 1.3379 |
- 0.0981 |
1.8113 |
0.9831 |
|
4 |
 |
- 0.6979 |
2.6728 |
- 0.2409 |
0.5453 |
- 1.0318 |
|
5 |
 |
0.6626 |
0.6263 |
0.5250 |
0.2441 |
- 1.6235 |
|
6 |
 |
2.2068 |
- 1.8784 |
- 0.0844 |
0.4282 |
- 0.4491 |
|
7 |
 |
- 1.1280 |
- 2.3814 |
0.4101 |
- 0.8967 |
0.0745 |
|
8 |
 |
1.5705 |
0.6324 |
- 0.5215 |
1.7308 |
- 1.2045 |
|
9 |
 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
|
10 |
 |
- 1.7388 |
- 1.1200 |
- 0.4732 |
0.2324 |
0.5331 |
|
11 |
 |
- 1.5543 |
- 0.5464 |
0.4042 |
1.2018 |
- 0.1983 |
|
12 |
 |
0.3185 |
- 0.4130 |
- 0.9820 |
- 1.1665 |
1.5478 |
|
13 |
 |
1.0055 |
1.0203 |
1.0400 |
1.0723 |
1.1873 |
|
14 |
 |
0.9850 |
0.9443 |
0.8905 |
0.8024 |
0.4932 |
|
15 |
 |
- 0.0547 |
- 0.2021 |
- 0.3971 |
- 0.7145 |
- 1.8141 |
|
16 |
 |
0.0819 |
0.3020 |
0.5910 |
1.0566 |
2.6174 |

Протокол построения форм колебаний балки принимает вид
х1 = 0 : 0.001 : 4.0; х2 = 0 : 0.001 : 6.0; х3 = 0 : 0.001 : 3.0;
х4 = 0 : 0.001 : 1.0; la = sqrt (0.4055125);
EIv1 = - (X(2,1)*(sinh(la*x1)+sin(la*x1))/(2*la) - …
X(4,1)*(sinh(la*x1)-sin(la*x1))/(2*la^3));
EIv2 = - (X(6,1)*(sinh(la*x2)+sin(la*x2))/(2*la) - …
X(7,1)*(cosh(la*x2)-cos(la*x2))/(2*la^2) - …
X(8,1)*(sinh(la*x2)-sin(la*x2))/(2*la^3));
EIv3 = - (X(10,1)*(sinh(la*x3)+sin(la*x3))/(2*la) - …
X(11,1)*(cosh(la*x3)-cos(la*x3))/(2*la^2) - …
X(12,1)*(sinh(la*x3)-sin(la*x3))/(2*la^3));
EIv4 = - (X(14,1)*(sinh(la*x4)+sin(la*x4))/(2*la) - …
X(15,1)*(cosh(la*x4)-cos(la*x4))/(2*la^2) - …
X(16,1)*(sinh(la*x4)-sin(la*x4))/(2*la^3));
subplot
(2,2,1), plot (x1, EIv1); axis ([0 4 - 0.5 0.5]); grid on
subplot
(2,2,2), plot (x2, EIv2); axis ([0 6 - 0.6 0.6]); grid on
subplot
(2,2,3), plot (x3, EIv3); axis ([0 3 - 0.5 0.5]); grid on
subplot
(2,2,4), plot (x4, EIv4); axis ([0 1 - 1 1 ]); grid on
Перед выполнением данного протокола из отдельного М-файла в окно команд помещается вектор Х -
вектор значений граничных параметров балки при wi . Выполняется это прогонкой программы, решающей систему уравнений (3.16). Далее отрабатывается протокол построения форм колебаний при собственной частоте wi . Первые 5 форм собственных колебаний балки при условии, что

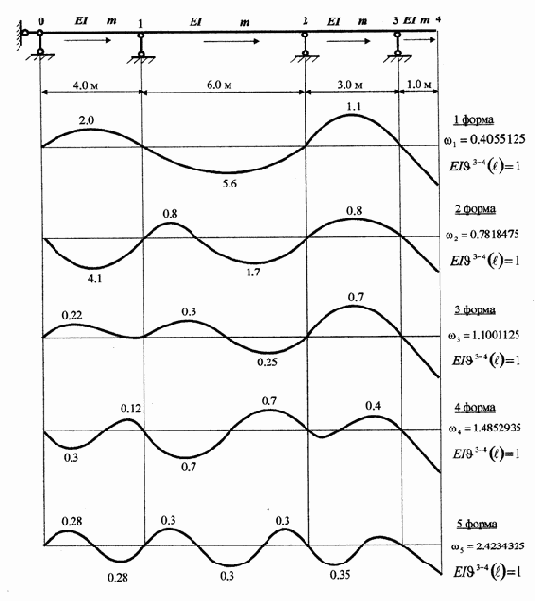 |
Добавим, что аналогично строятся формы колебаний для упругих систем, у которых узлы имеют только угловые перемещения. В этом случае граничные параметры могут нормироваться относительно угла поворота какого-либо граничного сечения.
3.2.5. Расчет на вынужденные колебания
 |
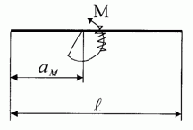 |
 |
(3.18) |
|
Рис. 3.8 |
||
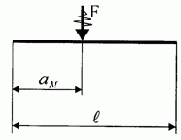 |
 |
(3.19) |
|
Рис. 3.9 |
||
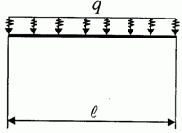
 |
 |
 |
(3.20) |
|
Рис. 3.10 |
= -
В, где матрица А повторяет матрицу частотного уравнения (см. п.3.2.3), а матрица В представлена в этом разделе. Программа также записывается в отдельном М-файле, куда переносится матрица А* задачи определения частот собственных колебаний и дополняется элементами вектора В. Сама программа имеет вид.
a = zeros (16,16); b =
zeros (16,1); X = zeros
(16,1); la = sqrt (0.1*0,315365);
l1 = 4.0; l2 =
6.0; l3 = 3.0; l4 = 1.0; m = 20.0; q = 10.0; f1 = - 40.0;
f2 = 60.0; am = 2.0; af1 = 2.0; af2 = 1.0;
a(1,2) = (sinh(la*l1) + sin (la*l1))/(2*la);
a(1,4) = - (sinh(la*l1) - sin (la*l1))/(2*la^3);
a(2,2) = (cosh(la*l1)+cos(la*l1))/2;
a(2,4) = - (cosh(la*l1) - cos (la*l1))/(2*la^2);
a(2,6) = - 1;
a(3,2) = la^ 4*a(1,4); a(3,4) = a(1,2); a(3,7) = - 1; a(4,1) = - 1;
a(4,2) = la^ 4*a(2,4); a(4,4) = a(2,2);
b(1,1) = - m* (cosh(la*(l1-am))- cos (la*(l1-am))) / (2*la^2);
b(2,1) = - m* (sinh(la*(l1-am)) + sin (la*(l1-am))) / (2*la);
b(3,1) = m* (cosh(la*(l1-am)) + cos (la*(l1-am))) / 2;
b(4,1) = m* la*(sinh(la*(l1-am)) - sin (la*(l1-am))) / 2;
a(5,6) = (sinh(la*l2) + sin (la*l2))/(2*la);
a(5,7)= - (cosh(la*l2) - cos(la*l2))/(2*la^2);
a(5,8) = - (sinh(la*l2) - sin (la*l2))/(2*la^ 3);
a(6,6)=(cosh(la*l2)+cos(la*l2))/2;
a(6,7) = -a(5,6); a(6,8) =a(5,7);
a(6,10) = -1; a(7,6) =la^ 4*a(5,8); a(7,7) =a(6,6); a(7,8) = a(5,6);
a(7,11) = - 1;
a(8,3) = - 1; a(8,6) = la^ 4*a(5,7); a(8,7) = - a(7,6);
a(8,8) = a(6,6);
b(5,1) = - q* (cosh(la*l2) + cos (la*l2) - 2) / (2*la^4);
b(6,1) = - q* (sinh(la*l2) - sin (la*l2)) / (2*la^3);
b(7,1) = q* (cosh(la*l2) - cos (la*l2)) / (2*la^2);
b(8,1) = q* (sinh(la*l2) + sin (la*l2)) / (2*la);
a(9,10) = (sinh(la*l3) + sin (la*l3))/(2*la);
a(9,11)= - (cosh(la*l3) -cos(la*l3))/(2*la^2);
a(9,12) =-(sinh(la*l3)-sin(la*l3))/(2*la^3);
a(10,10)=(cosh(la*l3)+cos(la*l3))/2;
a(10,11) = - a(9,10); a(10,12) = a(9,11);
a(10,14) = - 1; a(11,10) = la^ 4*a(9,12); a(11,11) =a(10,10); a(11,12)= a(9,10);
a(11,15)= -1; a(12,5)= -1; a(12,11) = - a(11,10); a(12,10)=la^ 4*a(9,11);
a(12,12)=a(10,10);
b(9,1) = - f1* (sinh(la*(l3-a f1))- sin (la*(l3-a f1))) / (2*la^3);
b(10,1) = - f1* (cosh(la*(l3-a f1)) - cos (la*(l3-a f1))) / (2*la^2);
b(11,1) = f1* (sinh(la*(l3-a f1)) + sin (la*(l3-a f1))) / (2*la);
b(12,1) = f1* (cosh(la*(l3-a f1)) + cos (la*(l3-a f1))) / 2; a(13,9) = - 1;
a(13,14)=(sinh(la*l4) + sin (la*l4))/(2*la);
a(13,15)= - (cosh(la*l4) -cos(la*l4))/(2*la^2);
a(13,16) = - (sinh(la*l4) - sin (la*l4))/(2*la^ 3); a(14,13) = - 1;
a(14,14)=(cosh(la*l4)+cos(la*l4))/2; a(14,15) = - a(13,14); a(14,16) =
a(13,15);
a(15,14) = la^ 4*a(13,16); a(15,15) = a(14,14); a(15,16) = a(13,14);
a(16,14) = la^ 4*a(13,15);
a(16,15) = - a(15,14); a(16,16) = a(14,14);
b(13,1) = - f2* (sinh(la*(l4-a f2))- sin (la*(l4-a f2))) / (2*la^3);
b(14,1) = - f2* (cosh(la* l4-a f2)) - cos (la*(l4-a f2))) / (2*la^2);
b(15,1) = f2* (sinh(la*(l4-a f2)) + cos (la*(l4-a f2))) / (2*la);
b(16,1) = f2* (cosh(la*(l4-a f2)) + cos (la*(l4-a f2))) / 2;
X = a\ b
Для ухода от резонанса частоту вынужденных колебаний принимаем

Тогда

Результаты расчета динамических граничных параметров балки
Таблица 3.3
|
Х = |
1 |
Х(1,1) =  |
|
2 |
Х(2,1) = |
|
|
3 |
Х(3,1) =  |
|
|
4 |
Х(4,1) = |
|
|
5 |
Х(5,1) = |
|
|
6 |
Х(6,1) =  |
|
|
7 |
Х(7,1) =  |
|
|
8 |
Х(8,1) =  |
|
|
9 |
Х(9,1) =  |
|
|
10 |
Х(10,1) =  |
|
|
11 |
Х(11,1) =  |
|
|
12 |
Х(12,1) =  |
|
|
13 |
Х(13,1) =  |
|
|
14 |
Х(14,1) =  |
|
|
15 |
Х(15,1) =  |
|
|
16 |
Х(16,1) =  |
/p>
3.2.6. Построение эпюр напряженно-деформированного состояния
балки при вынужденных колебаниях
Эпюры напряженно- деформированного состояния можно построить для каждого стержня в отдельности, используя соотношения метода начальных параметров.
 |
(3.21) |
 |
 |
(3.22) |
 |
 |
(3.22) |
 |
- единичная функция Хевисайда. |
аМ, аF, аH, аK – координаты внешней нагрузки.
Протоколы построения эпюр EIJ(x), EIj(x), M(x) и Q(x) примут вид
стержень 0-1
х = 0 : 0.0001 : 2.0; la = sqrt (0.1*0.315365);
EIv = - (X(2,1)*(sinh(la*x)+sin(la*x))/(2*la) - X(4,1)* …
(sinh(la*x)-sin(la*x))/(2*la^3));
EIfi = - (X(2,1)*(cosh(la*x)+cos(la*x)) / 2 - X(4,1)* …
(cosh(la*x)-cos(la*x))/(2*la^2));
Q = - X(2,1)*la^4*(cosh(la*x)-cos(la*x)) / (2*la^2) + …
X(4,1)* (cosh(la*x)+cos(la*x)) / 2;
M = - X(2,1)*la^4*(sinh(la*x)-sin(la*x))/(2*la^3) + …
X(4,1)*(sinh(la*x)+sin(la*x))/(2*la);
subplot
(2,2,1), plot (x, EIv); axis
([0 2 - 30 30]); grid on
subplot
(2,2,2), plot (x, EIfi); axis ([0 2 - 30 30]); grid on
subplot
(2,2,3), plot (x, Q); axis
([0 2 - 10 10]); grid on
subplot
(2,2,4), plot (x, M); axis
([0 2 - 3 3 ]); grid on
Перед выполнением этого протокола необходимо поместить в окно команд вектор граничных параметров Х (см. п. 3.2.5), значения нагрузки и их координаты.
х = 2.0 : 0.0001 : 4.0; m
= 20.0; am = 2.0; la = sqrt (0.1*0.315365);
EIv = - (X(2,1)*(sinh(la*x)+sin(la*x))/(2*la) - X(4,1)* …
(sinh(la*x)-sin(la*x))/(2*la^3)+m*(cosh(la*(x-am)) - …
cos (la*(x-am))) / (2*la^2));
EIfi = - (X(2,1)*(cosh(la*x)+cos(la*x)) / 2 -
X(4,1)*(cosh(la*x)- …
cos(la*x))/(2*la^2))+
m*(sinh(la*(x-am))+sin(la*(x-am))) / (2*la));
Q = - X(2,1)*la^4*(cosh(la*x)-cos(la*x)) / (2*la^2) + …
X(4,1)* (cosh(la*x)+cos(la*x)) / 2- m*(sinh(la*(x-am))- …
sin(la*(x-am)))*
la / 2;
M = - X(2,1)*la^4*(sinh(la*x)-sin(la*x))/(2*la^3) + X(4,1)* …
(sinh(la*x)+sin(la*x))/(2*la))- m*(cosh(la*(x-am)+ …
cos(la*(x-am))) / 2;
subplot
(2,2,1), plot (x, EIv); axis
([2 4 - 30 30]); grid on
subplot
(2,2,2), plot (x, EIfi); axis ([2 4 - 40 40]); grid on
subplot
(2,2,3), plot (x, Q); axis
([2 4 - 2 2]); grid on
subplot
(2,2,4), plot (x, M); axis
([2 4 - 30 30]); grid on
стержень 1-2
х = 0 : 0.0001 : 6.0; q = 10.0; la
= sqrt (0.1*0.315365);
EIv = - (X(6,1)*(sinh(la*x)+sin(la*x))/(2*la) - X(7,1)* …
(cosh(la*x)-cos(la*x))/(2*la^2)) -
X(8,1)*(sinh(la*x)-sin(la*x) …
) / (2*la^3)) + q* (cos(la*x) + cos(la*x) - 2) / (2*la^4));
EIfi = - (X(6,1)*(cosh(la*x)+cos(la*x)) / 2 - X(7,1)* (sinh(la*x) + …
sin(la*x)) / (2* la) - X(8,1)* (cosh(la*x) - cos(la*x)) / (2*la^2) + …
q*(sinh(la*x)-sin(la*x))/(2*la^3));
Q = - X(6,1)*la^4*(cosh(la*x)-cos(la*x)) / (2*la^2) + X(7,1)* …
la^4 *(sinh(la*x)-sin(la*x))/(2*la^3) + X(8,1)* (cosh(la*x) + cos(la*x) …
) / 2 - q*(sinh(la*x)+sin(la*x))/(2*la);
M = - X(6,1)*la^4*(sinh(la*x)-sin(la*x))/(2*la^3) + X(7,1)* …
(cosh(la*x)+cos(la*x)) / 2 + X(8,1)*(sinh(la*x)+sin(la*x))/(2*la) - …
q*(cosh(la*x)-cos(la*x)) / (2*la^2);
subplot
(2,2,1), plot (x, EIv); axis
([0 6 - 110 110]); grid on
subplot
(2,2,2), plot (x, EIfi); axis ([0 6 - 60 60]); grid on
subplot
(2,2,3), plot (x, Q); axis
([0 6 - 40 40]); grid on
subplot
(2,2,4), plot (x, M); axis
([0 6 - 40 40]); grid on
стержень 2-3
х = 0 : 0.0001 : 2.0; la = sqrt (0.1*0.315365);
EIv = - (X(10,1)*(sinh(la*x)+sin(la*x))/(2*la) - X(11,1)* ( …
cosh(la*x)-cos(la*x))/(2*la^2)-X(12,1)*(sinh(la*x)-sin(la*x)) …
/(2*la^3));
EIfi = - (X(10,1)*(cosh(la*x)+cos(la*x)) / 2 -
X(11,1)*(sinh(la*x) + …
sin(la*x))/(2*la) - X(12,1)*(cosh(la*x)-cos(la*x))/(2*la^2));
Q = - X(10,1)*(cosh(la*x)-cos(la*x))*la^4 / (2*la^2) + X(11,1)* …
la^4*(sinh(la*x)-sin(la*x))/(2*la^3) + X(12,1)*(cosh(la*x) + …
cos(la*x)) / 2;
M = - X(10,1)*(sinh(la*x)-sin(la*x))*la^4/(2*la^3) + X(11,1)* …
(cosh(la*x)+cos(la*x)) / 2 + X(12,1)*(sinh(la*x) +(sinh(la*x))/(2*la);
subplot
(2,2,1), plot (x, EIv); axis
([0 2 - 60 60]); grid on
subplot
(2,2,2), plot (x, EIfi); axis ([0 2 - 90 90]); grid on
subplot
(2,2,3), plot (x, Q); axis
([0 2 - 40 40]); grid on
subplot
(2,2,4), plot (x, M); axis
([0 2 - 70 70]); grid on
Протоколы эпюр второй части стержня имеют вид:
х = 2.0 : 0.0001 : 3.0; la
= sqrt (0.1*0.315365); f1 = - 40.0; af1 = 2.0;
EIv = - (X(10,1)*(sinh(la*x)+sin(la*x))/(2*la) - X(11,1)* ( …
cosh(la*x)-cos(la*x)) / (2*la^3) -
X(12,1)*(sinh(la*x)-sin(la*x)) …
/(2*la^3)+ f1*(sinh(la*(x-a f1))-sin(la*(x-a f1))) / (2*la^3));
EIfi = - (X(10,1)*(cosh(la*x)+cos(la*x)) / 2 -
X(11,1)*(sinh(la*x)+ …
sin(la*x))/(2*la)) - X(12,1)*(cosh(la*x) - cosh(la*x)) / (2*la^2) + …
f1*(cosh(la*(x-a f1))-cos(la*(x-a f1))) / (2*la^2));
Q = - X(10,1*(cosh(la*x)-cos(la*x))*la^4 / (2*la^2) + X(11,1)* …
la^4*(sinh(la*x)-sin(la*x))/(2*la^3) + X(12,1)*(cosh(la*x) + …
cos(la*x)) / 2 - f1*(cosh(la*(x-a f1))+cos(la*(x-a f1))) / 2;
M = - X(10,1)*(sinh(la*x)-sin(la*x))*la^4/(2*la^3) + X(11,1)* …
(cos(la*x)+ cos(la*x)) / 2 + X(12,1)*(sinh(la*x)+sin(la*x))/(2*la) …
- f1*(sinh(la*(x-a f1))+sin(la*(x-a f1))) / (2*la);
subplot
(2,2,1), plot (x, EIv); axis
([2 3 - 60 60]); grid on
subplot
(2,2,2), plot (x, EIfi); axis ([2 3 - 90 90]); grid on
subplot
(2,2,3), plot (x, Q); axis
([2 3 - 10 10]); grid on
subplot
(2,2,4), plot (x, M); axis
([2 3 - 70 70]); grid on
стержень 3-4
х = 0 : 0.0001 : 1.0; la = sqrt (0.1*0.315365);
EIv = - (X(14,1)*(sinh(la*x)+sin(la*x))/(2*la) -
X(15,1)*(cosh(la*x) …
-cos(la*x))/(2*la^2) - X(16,1)*(sinh(la*x)-sin(la*x))/(2*la^3));
EIfi = - (X(14,1)*(cosh(la*x)+cos(la*x)) / 2 -
X(15,1)*(sinh(la*x)+ …
sinh(la*x))/(2*la) - X(16,1)*(cosh(la*x)-cos(la*x))/(2*la^2));
Q = - X(14,1)*la^4*(cosh(la*x)-cos(la*x)) / (2*la^2) + X(16,1)* la^4* …
(sinh(la*x)-sin(la*x))/(2*la^3)+X(16,1)*(cosh(la*x)+cos(la*x)) / 2;
M=-X(14,1)*la^4*(sinh(la*x)-sin(la*x))/(2*la^3)+X(15,1)*(cosh(la*x)+…
cos(la*x))/2+X(16,1)*(sinh(la*x)+sin(la*x))/(2*la);
subplot
(2,2,1), plot (x, EIv); axis
([0 1 - 110 110]); grid on
subplot
(2,2,2), plot (x, EIfi); axis ([0 1 - 120 120]); grid on
subplot
(2,2,3), plot (x, Q); axis
([0 1 - 70 70]); grid on
subplot
(2,2,4), plot (x, M); axis
([0 1 - 70 70]); grid on
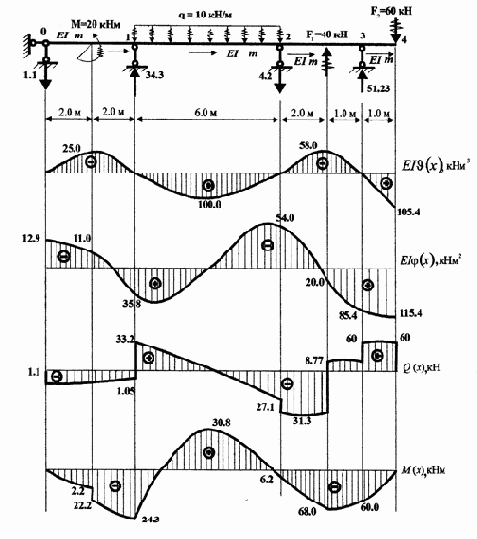
Анализ показывает, что несмотря на большой объем протоколов построения эпюр параметров балки, сам процесс довольно простой. В отдельном М-файле необходимо только дополнять недостающие элементы параметров и менять индексы вектора Х. Эпюры EIJ(x), EIj(x), Q(x) и М(x) представлены на рис. 3.7.
3.2.7. Определение критических сил потери устойчивости
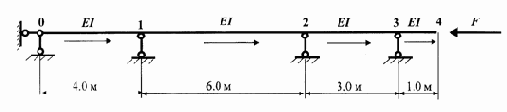 |
Исходные данные:

Матрица фундаментальных функций продольно-поперечного изгиба (задача устойчивости плоских стержневых систем)
 |
(3.23) |
|||||||||||
|
Аi = |
1 |
A12 |
-A13 |
-A14 |
|
|||||||
|
|
A22 |
-A12 |
-A13 |
|
||||||||
|
|
-A32 |
A22 |
A12 |
|
||||||||
|
|
|
|
1 |
|
||||||||
|
1 |
||||||||||||
/p> Критические силы определяются как корни трансцендентного уравнения êА*(F) ê
= 0, где матрицу А*
можно взять из задач статики или динамики данной балки с заменой фундаментальных функций. Для неразрезной балки можно не учитывать нормальные силы N, потому матрица А*(F) примет размер 16 ´ 16 строк и столбцов.
Корни (критические силы) можно определить методом последовательного перебора в сочетании с прямым ходом метода исключения Гаусса. Организуется цикл вычисления определителя êА*(F) ê, в конце которого величины F и d выводятся в окно команд. При просмотре таблицы значений F и d определяются точки, где изменяется знак определителя d = êА*(F) ê. Эти точки и есть критические силы потери устойчивости. Рекомендуется начинать вычисления с начального значения сжимающей силы F0
= 0.001 с шагом D
F = 0.001. Число вычислений определителя d = êА*(F) ê
п1 = 300 – 500 позволяет надежно и достаточно точно определить первую и старшие критические силы. При решении задачи принимаем, что EI = 1. Матрица устойчивости неразрезной балки принимает вид
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
| 3-4 |
| 2-3 |
| 1-2 |
| 0-1 |
А*(F)=
(3.24)
а – матрица А*(F); п – порядок матрицы А*(F); п1 – число циклов вычисления определителя d = êА*(F) ê; d – величина определителя; f – сжимающая сила F; df – шаг изменения сжимающей силы F; m – счетчик цикла вычисления определителя;

Текст программы
п = 16; п1 = 300; f = 0.01; df = 0.01; X = zeros
(n1,1); Y = zeros
(n1,1);
l1 = 4.0; l2 = 6.0; l3 = 3.0; l4 = 1.0;
for m = 1 : n1 п2 = sqrt (f); a = zeros (n,n);
a(1,2) = sin (п2*l1) / п2; a(1,4) = - (п2*l1-sin (п2*l1)) / (п2^3);
a(2,2)=cos (п2*l1); a(2,4) = - (1-cos (п2*l1)) / (п2^2); a(2,6) = - 1;
a(3,2) = п2*sin(п2*l1); a(3,7) = - 1; a(4,1) = - 1; a(4,4) = 1;
a(5,6) = sin (п2*l2) / п2; a(5,7)= - (1-cos (п2*l2)) / (п2^2);
a(5,8) = - (п2*l2-sin (п2*l2)) / (п2^ 3); a(6,6)=cos (п2*l2); a(6,7) = - a(5,6);
a(6,8) = a(5,7); a(6,10) = - 1; a(7,6) =
п2*sin(п2*l2); a(7,7) =
a(6,6);
a(7,8) = a(5,6); a(7,11) = - 1; a(8,3) = - 1; a(8,6) = 1; a(9,10) = (sin (п2*l3) / п2;
a(9,11)= - (1-cos (п2*l3)) / (п2^2); a(9,12) = - (п2*l3-sin (п2*l3)) / (п2^ 3);
a(10,10)=cos (п2*l3); a(10,11) = - a(9,10); a(10,12) = a(9,11); a(10,14) = - 1;
a(11,10) = п2*sin(п2*l3); a(11,11) = a(10,10); a(11,12) = a(9,10); a(11,15) = - 1;
a(12,5) = - 1; a(12,12) = 1; a(13,9) = - 1; a(13,14) = sin (п2*l4) / п2;
a(13,15)= - (1-cos (la*l4)) / (п2^2); a(13,16) = - (п2*l4-sin (п2*l4)) / (п2^ 3); a(14,13) = - 1; a(14,14)=cos (п2*l4); a(14,15) = - a(13,14); a(14,16) = a(13,15);
a(15,14) = п2*sin(п2*l4); a(15,15) = a(14,14); a(15,16) = a(13,14);
a(16,16) = 1; d = det(a); X(m,1) = f; Y(m,1) = d; f = f + df; end;
% Построение графика определителя матрицы устойчивости
plot (X,Y); grid on
% Вывод таблицы значений f и d в формате long e
format long e
[X Y]
График зависимости d = êА*(F) ê позволяет лишь грубо определить интервалы, где находятся корни (критические силы). Как и в динамике, этот график не имеет
точек разрыва 2-го рода (в методах сил и перемещений аналогичный график имеет разрывы 2-го рода) и служит вспомогательным средством при поиске критических сил. Уточнить критические силы можно при повторных прогонах программы (без построения графиков) с новыми интервалами для F.
Результаты поиска критических сил потери устойчивости

3.2.8. Построение форм потери устойчивости
Аналогично задаче динамики (п.3.2.4) примем, что b(16,1) = Q3-4(

Программа вычисления граничных параметров имеет вид
а = zeros
(16,16); b = zeros (16,1); X = zeros (16,1); п2 =sqrt(0.443685);
l1 = 4.0; l2 =
6.0; l3 = 3.0; l4 = 1.0;
a(1,2) =sin(п2*l1)/п2; a(1,4) = - (п2*l1-sin (п2*l1)) / (п2^3); a(2,2)=cos (п2*l1);
a(2,4) = - (1-cos (п2*l1)) / (п2^2); a(2,6) = - 1; a(3,2) = п2*sin(п2*l1);
a(3,4) = a(1,2); a(3,7) = - 1; a(4,1) = - 1; a(4,4) = 1;
a(5,6) = sin (п2*l2) / п2; a(5,7)= - (1-cos (п2*l2)) / (п2^2);
a(5,8) = - (п2*l2-sin (п2*l2)) / (п2^ 3); a(6,6)=cos (п2*l2); a(6,7) = - a(5,6);
a(6,8) = a(5,7); a(6,10) = - 1; a(7,6) =
п2*sin(п2*l2); a(7,7) =
a(6,6);
a(7,8) = a(5,6); a(7,11) = - 1; a(8,3) = - 1; a(8,8) = 1;
a(9,10) = sin (п2*l3) / п2; a(9,11)= - (1-cos (п2*l3)) / (п2^2);
a(9,12) = - (п2*l3-sin (п2*l3)) / (п2^ 3); a(10,10)=cos (п2*l3);
a(10,11) = - a(9,10); a(10,12) = a(9,11); a(10,14) = - 1;
a(11,10) = п2*sin(п2*l3); a(11,11) = a(10,10); a(11,12) = a(9,10);
a(11,15) = - 1; a(12,5) = - 1; a(12,12) = 1; a(13,9) = - 1;
a(13,14) = sin (п2*l4) / п2; a(13,15)= - (1-cos (la*l4)) / (п2^2);
a(13,16) = - (п2*l4-sin (п2*l4)) / (п2^ 3); a(14,13) = - 1;
a(14,14)=cos (п2*l4); a(14,15) = - a(13,14);
a(14,16) = a(13,15);
a(15,14) = п2*sin(п2*l4); a(15,15) = a(14,14); a(15,16) = a(13,14);
a(16,16) = 1; b (16,1) = 1; X = a\ b; X = X / X(9,1)
Результаты вычислений относительных значений граничных параметров балки при потере устойчивости сведены в таблицу 3.4.
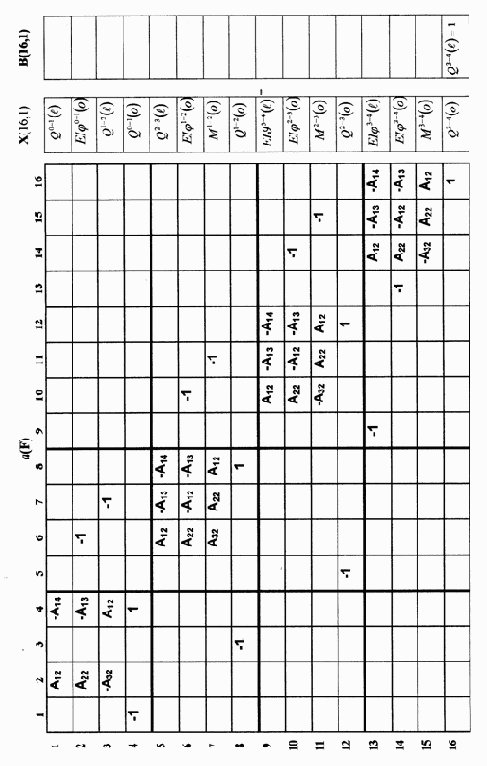 |
(3.25) |
|
№ п/п |
Относительные граничные параметры балки |
Относительные формы потери устойчивости при критических силах |
||||
|
F1=0,443685 |
F2=0,6525565 |
F3=1,051035 |
F4=1,618795 |
F5=2,430485 |
||
|
1 |
 |
-0.05447 |
-0.0103 |
0.2820 |
-0.5033 |
0.0329 |
|
2 |
 |
-0.5915 |
0.5841 |
-1.6119 |
2.0126 |
-1.8039 |
|
3 |
 |
-0.0026 |
0.0659 |
-0.0127 |
0.5231 |
-0.0775 |
|
4 |
 |
-0.0547 |
-0.0103 |
0.2820 |
-0.5033 |
0.0329 |
|
5 |
 |
0.0697 |
-0.3356 |
-0.7009 |
-0.9147 |
-0.6990 |
|
6 |
 |
0.7580 |
-0.5503 |
0.5032 |
0.9372 |
-1.8019 |
|
7 |
 |
-0.2186 |
-0.0411 |
1.1278 |
-2.0131 |
0.1316 |
|
8 |
 |
-0.0026 |
0.0659 |
-0.0127 |
0.5231 |
-0.0775 |
|
9 |
 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
|
10 |
 |
-0.7352 |
-0.2117 |
0.6437 |
1.4961 |
1.8552 |
|
11 |
 |
-0.2345 |
0.3542 |
1.0518 |
1.1254 |
-0.3335 |
|
12 |
 |
-0.0697 |
-0.3356 |
-0.7009 |
-0.9147 |
-0.6990 |
|
13 |
 |
1.0780 |
1.1177 |
1.1993 |
1.3312 |
1.5591 |
|
14 |
 |
0.8475 |
0.7724 |
0.6224 |
0.3914 |
0.0184 |
|
15 |
 |
-0.4437 |
-0.6526 |
-1.0510 |
-1.6189 |
-2.4305 |
|
16 |
 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
/p> Выражение для прогиба ( формы потери устойчивости) согласно методу начальных параметров имеет вид

Протокол построения форм потери устойчивости запишется в виде
х1 = 0 : 0.001 : 4.0; х2 = 0 : 0.001 : 6.0; х3 = 0 : 0.001 : 3.0;
х4 = 0 : 0.001 : 1.0; п2 = sqrt (0.443685);
EIv1 = - (X(2,1)*(sin(п2*x1) / п2 - X(4,1)*(п2*x1-sin(п2*x1)) …
/ п2^3);
EIv2 = - (X(6,1)*sin(п2*x2) / п2 -
X(7,1)*(1-cos(п2*x2)) / п2^2) - …
X(8,1)*( п2*x2-sin(п2*x2)) / п2^3);
EIv3 = - (X(10,1)*sin(п2*x3) / п2 -
X(11,1)*(1-cos(п2*x3)) / п2^2) - …
X(12,1)*( п2*x3-sin(п2*x3)) / п2^3);
EIv4 = - (X(14,1)*sin(п2*x4) / п2 -
X(15,1)*(1-cos(п2*x4)) / п2^2 - …
X(16,1)*( п2*x4-sin(п2*x4)) / п2^3);
subplot
(2,2,1), plot (x1, EIv1); axis ([0 4 - 2 2]); grid on
subplot
(2,2,2), plot (x2, EIv2); axis ([0 6 - 2 2]); grid on
subplot
(2,2,3), plot (x3, EIv3); axis ([0 3 - 2 2]); grid on
subplot
(2,2,4), plot (x4, EIv4); axis ([0 1 - 2 2]); grid on
Перед выполнением данного протокола из отдельного М-файла в окно команд помещается вектор Х -
вектор относительных значений граничных параметров балки. Выполняется это прогонкой программы, решающей систему уравнений (3.25). Далее нужно задействовать протокол построения форм потери устойчивости балки при разных критических силах Fi. Первые 5 форм потери устойчивости балки при условии, что

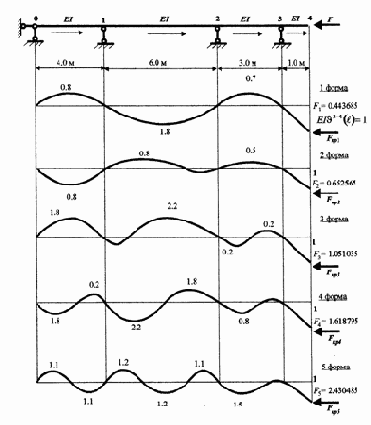 |
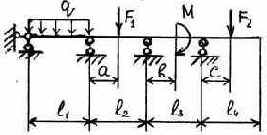
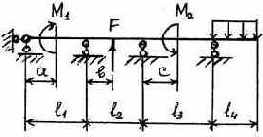
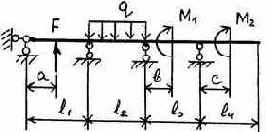
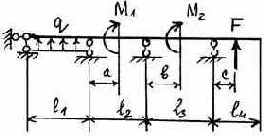
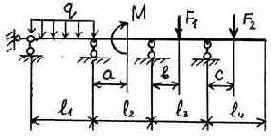
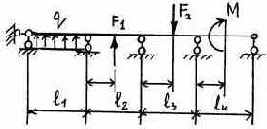
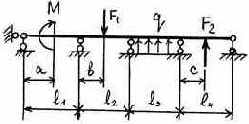
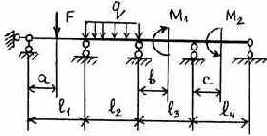
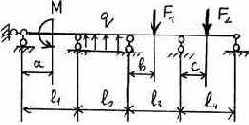
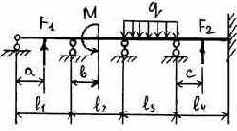
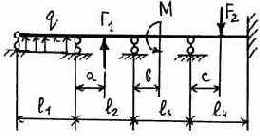
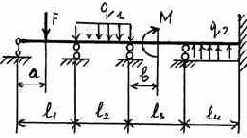
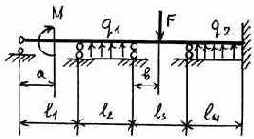
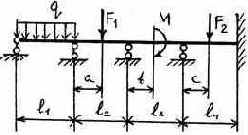
3.2.9. Варианты заданий
|
1 |
2 |
 |
 |
|
3 |
4 |
 |
 |
|
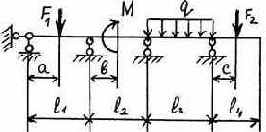
5 |
6 |
 |
 |
|
7 |
8 |
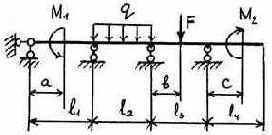 |
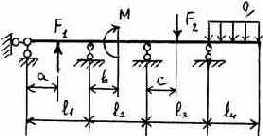 |
|
9 |
10 |
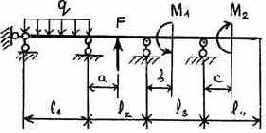 |
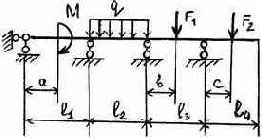 |
|
11 |
12 |
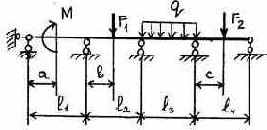 |
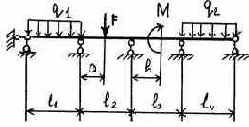 |
|
13 |
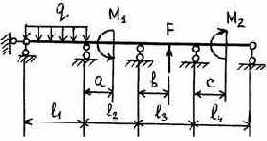
14 |
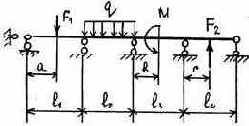
 |
 |
|
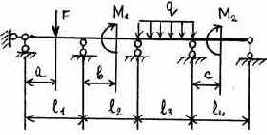
15 |
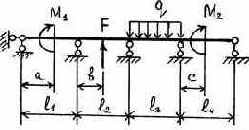
16 |
 |
 |
|
17 |
18 |
 |
 |
|
19 |
20 |
 |
 |
|
21 |
22 |
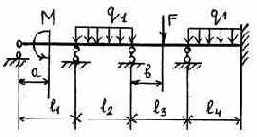 |
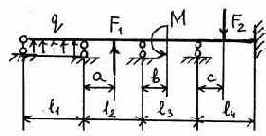 |
|
23 |
24 |
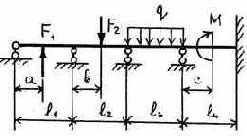 |
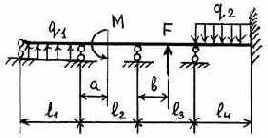 |
|
25 |
26 |
 |
 |
|
27 |
28 |
 |
 |
|
29 |
30 |
 |
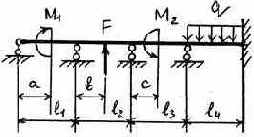 |
Таблица 3.5
Исходные данные к расчету неразрезной балки
|
№ варианта заданий |
 |
 |
 |
 |
a |
b |
c |
F |
F1 |
F2 |
M |
M1 |
M2 |
q |
q1 |
q2 |
|
м |
кН |
кНм |
кН/м |
|||||||||||||
|
1 |
2 |
3 |
3 |
1 |
1 |
2 |
1 |
10 |
20 |
30 |
6 |
8 |
10 |
10 |
12 |
8 |
|
2 |
2 |
4 |
4 |
2 |
2 |
1 |
2 |
40 |
50 |
60 |
10 |
8 |
6 |
8 |
15 |
6 |
|
3 |
4 |
3 |
5 |
1,5 |
3 |
3 |
1,5 |
5 |
15 |
20 |
20 |
30 |
40 |
6 |
10 |
12 |
|
4 |
5 |
6 |
6 |
3 |
2 |
2 |
3 |
25 |
35 |
45 |
25 |
36 |
38 |
4 |
8 |
6 |
|
5 |
6 |
8 |
7 |
2,5 |
1 |
1 |
1 |
10 |
8 |
6 |
12 |
6 |
18 |
2 |
4 |
3 |
|
6 |
7 |
5 |
8 |
1 |
3 |
2,5 |
1,5 |
10 |
15 |
25 |
15 |
20 |
25 |
12 |
2 |
7 |
|
7 |
6 |
4 |
7 |
1,5 |
1 |
1,5 |
2,5 |
30 |
40 |
50 |
40 |
35 |
16 |
20 |
8 |
10 |
|
8 |
5 |
3 |
6 |
2 |
2 |
2 |
1,5 |
60 |
70 |
80 |
10 |
15 |
20 |
15 |
12 |
15 |
|
9 |
4 |
4 |
5 |
1 |
1,5 |
1 |
2 |
30 |
15 |
18 |
25 |
30 |
35 |
12 |
2 |
5 |
|
10 |
3 |
6 |
4 |
1,5 |
3 |
1,5 |
1 |
28 |
32 |
24 |
40 |
45 |
50 |
8 |
4 |
10 |
|
11 |
2,5 |
5 |
5 |
1 |
2 |
1,5 |
1,5 |
12 |
14 |
16 |
10 |
18 |
28 |
6 |
8 |
15 |
|
12 |
4 |
8 |
3 |
2,8 |
1 |
1,5 |
2 |
5 |
15 |
10 |
40 |
12 |
10 |
10 |
12 |
2 |
|
13 |
3 |
10 |
4 |
4 |
1 |
2 |
2 |
3 |
22 |
30 |
10 |
14 |
16 |
18 |
12 |
14 |
|
14 |
5 |
4 |
5 |
2 |
1 |
1,5 |
1,6 |
40 |
24 |
26 |
20 |
30 |
35 |
10 |
30 |
15 |
|
15 |
2 |
5 |
6 |
1,5 |
1,7 |
1,5 |
1,2 |
15 |
10 |
8 |
15 |
18 |
20 |
5 |
20 |
10 |
|
16 |
2 |
6 |
3 |
1 |
0,8 |
1,4 |
1,0 |
10 |
20 |
30 |
6 |
8 |
10 |
10 |
12 |
8 |
|
17 |
3 |
7 |
4 |
5 |
2 |
1 |
2 |
40 |
50 |
60 |
10 |
8 |
6 |
8 |
15 |
6 |
|
18 |
4 |
5 |
5 |
1,5 |
3 |
3 |
1,5 |
5 |
15 |
20 |
20 |
30 |
40 |
6 |
10 |
12 |
|
19 |
5 |
3 |
6 |
3 |
2 |
2 |
1,5 |
25 |
35 |
45 |
25 |
36 |
38 |
4 |
8 |
6 |
|
20 |
6 |
5 |
5 |
2,5 |
1 |
1 |
1 |
10 |
8 |
6 |
12 |
6 |
18 |
2 |
4 |
3 |
|
21 |
7 |
4 |
7 |
1 |
3 |
1,5 |
1,5 |
10 |
25 |
35 |
15 |
20 |
25 |
12 |
2 |
7 |
|
22 |
6 |
8 |
6 |
1,5 |
1 |
2 |
2,5 |
30 |
40 |
50 |
40 |
35 |
16 |
20 |
8 |
10 |
|
23 |
5 |
6 |
5 |
2 |
2 |
2 |
1,2 |
60 |
70 |
80 |
10 |
15 |
20 |
15 |
12 |
15 |
|
24 |
4 |
7 |
4 |
1 |
1,5 |
1 |
2 |
30 |
15 |
18 |
25 |
30 |
35 |
12 |
2 |
5 |
|
25 |
3 |
5 |
3 |
1,5 |
3 |
1,5 |
1 |
28 |
32 |
24 |
40 |
45 |
50 |
8 |
4 |
10 |
|
26 |
2 |
4 |
4 |
1 |
1,3 |
1,4 |
1,5 |
12 |
14 |
16 |
10 |
18 |
28 |
6 |
8 |
15 |
|
27 |
4 |
6 |
3 |
2 |
1 |
1,5 |
1,7 |
5 |
15 |
10 |
40 |
12 |
10 |
10 |
12 |
2 |
|
28 |
3 |
5 |
4 |
4 |
1 |
2 |
2 |
3 |
22 |
30 |
10 |
14 |
16 |
18 |
12 |
14 |
|
29 |
5 |
4 |
5 |
2 |
1 |
1,5 |
1,5 |
40 |
24 |
26 |
20 |
30 |
35 |
10 |
30 |
15 |
|
30 |
2 |
3 |
6 |
4 |
1,5 |
2 |
1 |
15 |
10 |
8 |
15 |
18 |
20 |
5 |
20 |
10 |
3.3. Расчет плоской рамы
3.3.1. Определение граничных параметров при статической
нагрузке
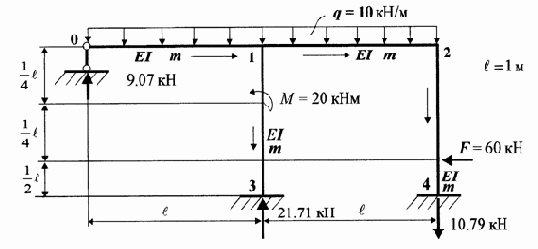 |






